陕西省西安市碑林区2021-2022学年八年级上学期期中数学试题

试卷更新日期：2022-10-09 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各数中，是无理数的是（）

A、 $\sqrt{15}$ B、3.141592 C、 $\frac{13}{5}$ D、 $\sqrt{16}$

查看试题解析
2. 下列各组数中，以它们为边长的线段能构成直角三角形的是（）

A、1，2，3 B、1， $\sqrt{2}$ ， $\sqrt{3}$ C、4，5，6 D、12，15，20

查看试题解析
3. 下列曲线中，表示y是x的函数的是（）

A、 B、 C、 D、

查看试题解析
4. 若代数式 $\frac{\sqrt{2 x + 8}}{3}$ 有意义，则x的值可能为（）

A、 $- 8$ B、 $- 5$ C、0 D、 $- 10$

查看试题解析
5. 如图，在平面直角坐标系中，已知“蝴蝶”上有两点 $A (3 ， 7)$ ， $B (7 ， 7)$ ，将该“蝴蝶”经过平移后点A的对应点为 $A^{^{'}} (1 ， 3)$ ，则点B的对应点 $B^{'}$ 的坐标为（）

A、 $(9 ， 11)$ B、 $(9 ， 3)$ C、 $(3 ， 5)$ D、 $(5 ， 3)$

查看试题解析
6. 下列式子计算正确的是（）

A、 $\sqrt{3} + \sqrt{7} = \sqrt{10}$ B、 $\sqrt{8} - \sqrt{2} = \sqrt{2}$ C、 $\sqrt{5} \times \sqrt{2} = 10$ D、 $\sqrt{12} \div \sqrt{3} = 4$

查看试题解析
7. 若点 $A (2 ， m)$ 在一次函数 $y = 2 x - 7$ 的图象上，则点A到x轴的距离是（）

A、2 B、 $- 2$ C、3 D、 $- 3$

查看试题解析
8. 有一个面积为1的正方形，经过一次“生长”后，在它的左右肩上“生长”出两个小正方形，其中，三个正方形围成的三角形是直角三角形，再经过一次“生长”后，变成了如图所示的形状图，如果继续“生长”下去，它将变得“枝繁叶茂”，请你算出“生长”了888次后形成的图形中所有的正方形的面积和是（）

A、445 B、887 C、888 D、889

查看试题解析

二、填空题

9. 将 $\frac{3}{\sqrt{2}}$ 化为最简二次根式为．

查看试题解析
10. 如图，有一个英文单词，它的各个字母的位置依次是 $(1 ， 2)$ ， $(5 ， 1)$ ， $(1 ， 1)$ ， $(5 ， 2)$ ， $(6 ， 3)$ ， $(1 ， 2)$ 所对应的字母，如 $(4 ， 2)$ 对应的字母是K，则这个英文单词为．

查看试题解析
11. 已知点 $P (2 m - 10 ， 3 m - 9)$ 在第二象限，且离x轴的距离为3，则 $| m + 3 | + | m - 5 | =$ ．

查看试题解析
12. 某图书馆对外出租书的收费方式是：每本书出租后的前两天，每天收0.6元，以后每天收0.3元，那么一本书在出租后x天 $(x ⩾ 2)$ 后，所收租金y与天数x的表达式为．

查看试题解析
13. 如图，在四边形 $A B C D$ 中，E为 $A B$ 的中点， $D E ⊥ A B$ 于点E， $A B = 8$ ， $D E = \sqrt{5}$ ， $B C = 2$ ， $C D = 5$ ，则四边形 $A B C D$ 的面积为．

查看试题解析

三、解答题

14. 计算： $\sqrt[3]{27} + \sqrt{18} \times (\sqrt{\frac{1}{2}} + \sqrt{\frac{9}{8}})$ ．

查看试题解析
15. 计算： $(\sqrt{3} + \sqrt{5})^{2} + (\sqrt{13} + \sqrt{7}) (\sqrt{13} - \sqrt{7}) - (\sqrt{75} \div \sqrt{3} - \sqrt{15})$ ．

查看试题解析
16. 已知关于x的函数 $y = (m + 2) x^{| m | - 1} + n - 5$ ，当m，n为何值时，它是正比例函数？

查看试题解析
17. 如图在平面直角坐标系中， $Δ A B C$ 各顶点的坐标分别为： $A (4 ， 0)$ ， $B (- 1 ， 4)$ ， $C (- 3 ， 1)$

(1)、在图中作△ $A^{'} B^{'} C^{'}$ ，使△ $A^{'} B^{'} C^{'}$ 和 $Δ A B C$ 关于 $x$ 轴对称；

(2)、写出点 $A ′$ ， $B ′$ ， $C^{'}$ 的坐标；

(3)、求 $Δ A B C$ 的面积．

查看试题解析
18. 如图，已知 $∠ B = ∠ D = 90 °$ ， $A D = 24$ ， $D C = 7$ ， $A B = 16$ ，求 $B C$ 的长．

查看试题解析
19. 已知点 $P (\frac{3}{2} a + 2$ ， $2 a - 3)$ ，根据下列条件，求出点P的坐标．

(1)、点P在y轴上；

(2)、点Q的坐标为 $(- 3 ， a)$ ，直线 $P Q / / x$ 轴．

查看试题解析
20. 已知 $M = \sqrt[3 m + 2 n + 1]{14 n - 3}$ 是 $14 n - 3$ 的算术平方根， $N = \sqrt[2 m + 5]{m + 65}$ 是 $m + 65$ 的立方根，求 $(N - M)^{2021}$ 的值．

查看试题解析
21. 已知y是关于x的一次函数，如表列出了部分对应值：
$x$
$\dots$
$- 2$
$- 1$
0
1
$b$
$\dots$
$y$
$\dots$
$- 8$
$a$
$- 2$
1
4
$\dots$

(1)、求此一次函数的表达式；

(2)、求a，b的值．

查看试题解析
22. 阅读下列内容：因为 $1 < 3 < 9$ ，所以 $1 < \sqrt{3} < 3$ ，所以 $\sqrt{3}$ 的整数部分是1，小数部分是 $\sqrt{3} - 1$ ．试解决下列问题：

(1)、求 $\sqrt{11}$ 的整数部分和小数部分；

(2)、若已知 $8 + \sqrt{13}$ 的小数部分是a， $8 - \sqrt{13}$ 的整数部分是b，求 $a b - 3 a + 4 b$ 的值．

查看试题解析
23. 为了积极宣传防疫，某区政府采用了移动车进行广播，如图，小明家在南大街这条笔直的公路 $M N$ 的一侧点A处，小明家到公路 $M N$ 的距离 $A B$ 为 $600$ 米，假使广播车P周围 $1000$ 米以内能听到广播宣传，广播车P以 $250$ 米/分的速度在公路 $M N$ 上沿 $P N$ 方向行驶时，假如小明此时在家，他是否能听到广播宣传？若能，请求出他总共能斪到多长时间的广播宣传？若不能，请说明理由.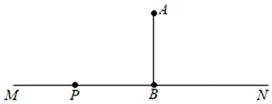

查看试题解析
24. 水是人们赖以生存的重要资源，保护水资源是我们每个人的责任，除了平时节约用水，污水净化也是保护水资源的方法之一．某企业生产的产品每件出厂价为50元，成本价为25元，在生产过程中，平均每生产一件产品就有 $0.5 m^{3}$ 的污水排出，为了绿色环保达到排污标准，工厂设计了两种处理污水的方案：
方案一：工厂污水先净化处理后再排出，每处理 $1 m^{3}$ 污水的费用为2元，并且每月排污设备损耗为20000元；
方案二：工厂将污水排到污水净化厂统一处理，每处理 $1 m^{3}$ 污水的费用为12元．

(1)、设工厂每月生产x件产品，每月利润为y元，分别写出依据方案一和方案二处理污水时，y与x的关系式；

(2)、若11月份计划生产5000件该产品，选择哪个方案获得的利润较大？

查看试题解析
25. 先观察下列等式，再回答下列问题：
① $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} = 1 + \frac{1}{1} - \frac{1}{2} = 1 \frac{1}{2}$ ；
② $\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} = 1 + \frac{1}{2} - \frac{1}{3} = 1 \frac{1}{6}$ ；
③ $\sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} = 1 + \frac{1}{3} - \frac{1}{4} = 1 \frac{1}{12}$ ．

(1)、请你根据上面三个等式提供的信息，猜想 $\sqrt{1 + \frac{1}{5^{2}} + \frac{1}{6^{2}}}$ 的结果，并验证；

(2)、请利用上述规律来计算 $\sqrt{\frac{50}{49} + \frac{1}{64}}$ （仿照上式写出过程）；

(3)、请你按照上面各等式反映的规律，试写出一个用 $m (m$ 为正整数）表示的等式．

查看试题解析
26. 对于平面直角坐标系 $x O y$ 中的点 $A (x ， y)$ ，给出如下定义，若存在点 $B (x \pm a$ ， $y \pm a) (a$ 为正数），称点B为点A的等距点．例如：如图，对于点 $A (1 ， 1)$ ，存在点 $B (3 ， 3)$ ，点 $C (- 1 ， 3)$ ，则点B，C分别为点A的等距点．

(1)、若点A的坐标是 $(0 ， 1)$ ，写出当 $a = 4$ 时，点A在第一象限的等距点坐标；

(2)、若点A的等距点B的坐标是 $(- 3 ， 1)$ ，求当点A的横、纵坐标相同时的坐标；

(3)、是否存在a的值，当将某个点 $A (x ， y)$ 的所有等距点用线段依次连接起来所得到的长方形的周长为 $\frac{25}{4}$ ，若存在，请求出a的值；若不存在，请说明理由．

查看试题解析

$x$	$\dots$	$- 2$	$- 1$	0	1	$b$	$\dots$
$y$	$\dots$	$- 8$	$a$	$- 2$	1	4	$\dots$