广西壮族自治区崇左市宁明县2021-2022学年八年级上学期期中数学试题
试卷更新日期:2022-10-09 类型:期中考试
一、单选题
-
1. 点P在第二象限内,P到x轴的距离是2,到y轴的距离是3,那么点P的坐标为( )A、(-2,3) B、(-3,-2) C、(-3,2) D、(3,-2)2. △ABC的三条边长分别是a、b、c,则下列各式成立的是( )A、 B、 C、 D、3. 下列语句中,是命题的是( )A、∠α和∠β相等吗 B、两个锐角的和大于直角 C、作∠A的平分线MN D、在线段AB上任取一点4. 在同一直角坐标系中,若直线与直线平行,则( )A、 , B、 , C、 , D、 ,5. 若一个正比例函数的图象经过A(3,﹣6),B(m,﹣4)两点,则m的值为( )A、2 B、8 C、﹣2 D、﹣86. 一个三角形三条边长度的比为2:3:4,且其中一条边长是12cm,这个三角形周长不可能是: ( )A、54cm B、36cm C、27cm D、24cm7. 如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=( )
 A、90° B、180° C、270° D、360°8. 将点A(3,2)沿x轴向左平移4个单位长度得到点A′,点A′关于y轴对称的点的坐标是( )A、(﹣3,2) B、(﹣1,2) C、(1,2) D、(1,﹣2)9. 以下是四位同学在钝角三角形ABC中画BC边上的高,其中画法正确的是( )A、
A、90° B、180° C、270° D、360°8. 将点A(3,2)沿x轴向左平移4个单位长度得到点A′,点A′关于y轴对称的点的坐标是( )A、(﹣3,2) B、(﹣1,2) C、(1,2) D、(1,﹣2)9. 以下是四位同学在钝角三角形ABC中画BC边上的高,其中画法正确的是( )A、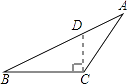 B、
B、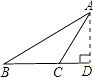 C、
C、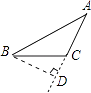 D、
D、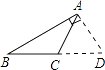 10. 已知点 、点 在一次函数 的图像上,且 ,则m的取值范围是( )A、 B、 C、 D、11. 如图,一次函数y1=x+3与y2=ax+b的图象相交于点P(1,4),则关于x的不等式x+3≤ax+b的解集是( )
10. 已知点 、点 在一次函数 的图像上,且 ,则m的取值范围是( )A、 B、 C、 D、11. 如图,一次函数y1=x+3与y2=ax+b的图象相交于点P(1,4),则关于x的不等式x+3≤ax+b的解集是( ) A、x≥4 B、x≤4 C、x≥1 D、x≤112. 一盘蚊香长100cm , 点燃时每小时缩短10cm , 小明在蚊香点燃5h后将它熄灭,过了2h , 他再次点燃了蚊香.下列四个图象中,大致能表示蚊香剩余长度y(cm)与所经过时间x(h)之间的函数关系的是( )A、
A、x≥4 B、x≤4 C、x≥1 D、x≤112. 一盘蚊香长100cm , 点燃时每小时缩短10cm , 小明在蚊香点燃5h后将它熄灭,过了2h , 他再次点燃了蚊香.下列四个图象中,大致能表示蚊香剩余长度y(cm)与所经过时间x(h)之间的函数关系的是( )A、 B、
B、 C、
C、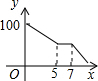 D、
D、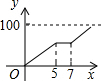
二、填空题
-
13. 如果将电影票上“6排3号”简记为(6,3),那么“9排21号”可表示为 .
14. 若点P(1,a)与Q(b,2)关于x轴对称,则代数式(a+b)2021的值为 .15. 等腰三角形的三边长为3,a , 7,则它的周长是 .
16. 当k= 时,函数y=是关于x的一次函数.17. 李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长度恰好为24米.要围成的菜园是如图所示的长方形ABCD,设BC边的长为x米,AB边的长为y米,则y与x之间的函数关系式是 . 18. 如图,在△ABC中,已知点D为BC边上一点,E、F分别为边AD、CE的中点,且S△ABC=8cm2 , 则S阴影=cm2 .
18. 如图,在△ABC中,已知点D为BC边上一点,E、F分别为边AD、CE的中点,且S△ABC=8cm2 , 则S阴影=cm2 .
三、解答题
-
19. 如图,已知△ABC三个顶点的坐标分A(﹣3,2),B(﹣1,3),C(﹣2,1).将△ABC先向右平移4个单位,再向下平移3个单位后,得到△A′B′C′,点A,B,C的对应点分别为A′、B′、C′.
 (1)、根据要求在网格中画出相应图形;(2)、写出△A′B′C′三个顶点的坐标.20. 如图,在△ABC中,AD是BC边上的中线,△ABD的周长比△ADC的周长多2,且AB与AC的和为10.
(1)、根据要求在网格中画出相应图形;(2)、写出△A′B′C′三个顶点的坐标.20. 如图,在△ABC中,AD是BC边上的中线,△ABD的周长比△ADC的周长多2,且AB与AC的和为10.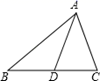 (1)、求AB、AC的长;(2)、求BC边的取值范围.21. 如图为某校区分布图的一部分,方格纸中每个小方格是边长为1个单位的正方形,若教学楼的坐标为A(1,2),图书馆的坐标为(-2,-1).解答以下问题:
(1)、求AB、AC的长;(2)、求BC边的取值范围.21. 如图为某校区分布图的一部分,方格纸中每个小方格是边长为1个单位的正方形,若教学楼的坐标为A(1,2),图书馆的坐标为(-2,-1).解答以下问题:
( 1 )在图中找到坐标系中的原点O,并建立直角坐标系;
( 2 )若体育馆的坐标为C(1,-3),食堂坐标为D (2,0),请在图中标出体育馆和食堂的位置;
( 3 )顺次连接教学楼、图书馆、体育馆、食堂得到四边形ABCD,求四边形ABCD的面积.22. 一次函数y=kx+b图象经过点(1,3)和(4,6)①试求k与b;
②画出这个一次函数图象;

③这个一次函数与y轴交点坐标是( )
④当x 时,y<0.
23. 如图,在△ABC中,CD、CE分别是△ABC的高和角平分线. (1)、若∠A=30°,∠B=50°,求∠ECD的度数;(2)、试用含有∠A、∠B的代数式表示∠ECD(不必证明)24. 为响应绿色出行号召,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式.下图描述了两种方式应支付金额y(元)与骑行时间x(时)之间的函数关系.根据图象回答下列问题.
(1)、若∠A=30°,∠B=50°,求∠ECD的度数;(2)、试用含有∠A、∠B的代数式表示∠ECD(不必证明)24. 为响应绿色出行号召,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式.下图描述了两种方式应支付金额y(元)与骑行时间x(时)之间的函数关系.根据图象回答下列问题. (1)、求手机支付金额y(元)与骑行时间x(时)的函数关系式;(2)、李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.25. 某酒厂每天生产A,B两种品牌的白酒共600瓶,A,B两种品牌的白酒每瓶的成本和利润如下表:设每天生产A种品牌白酒x瓶,每天获利y元.
(1)、求手机支付金额y(元)与骑行时间x(时)的函数关系式;(2)、李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.25. 某酒厂每天生产A,B两种品牌的白酒共600瓶,A,B两种品牌的白酒每瓶的成本和利润如下表:设每天生产A种品牌白酒x瓶,每天获利y元.A
B
成本(元/瓶)
50
35
利润(元/瓶)
20
15
(1)、请写出y关于x的函数关系式;(2)、如果该酒厂每天至少投入成本26400元,那么每天至少获利多少元?26. “8字”的性质及应用: (1)、如图①,AD、BC相交于点O , 得到一个“8字”ABCD , 求证:∠A+∠B=∠C+∠D .(2)、图②中共有多少个“8字”?(3)、如图②,∠ABC和∠ADC的平分线相交于点E , 利用(1)中的结论证明∠E= (∠A+∠C).
(1)、如图①,AD、BC相交于点O , 得到一个“8字”ABCD , 求证:∠A+∠B=∠C+∠D .(2)、图②中共有多少个“8字”?(3)、如图②,∠ABC和∠ADC的平分线相交于点E , 利用(1)中的结论证明∠E= (∠A+∠C).