吉林省长春市双阳区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中，不是无理数的是（）

A、 $\sqrt{2}$ B、0.5 C、2 $π$ D、 $\sqrt[3]{15}$

查看试题解析
2. 0.49的平方根是（）

A、 $- 0.7$ B、 $0.7$ C、 $\pm 0.7$ D、 $0.49$

查看试题解析
3. $a^{2} . a^{3}$ 等于（）

A、 $a^{5}$ B、 $a^{6}$ C、 $a^{8}$ D、 $a^{9}$

查看试题解析
4. 估计 $\sqrt{11}$ 的值在（）

A、1到2之间 B、2到3之间 C、3到4之间 D、4到5之间

查看试题解析
5. 如图是护士统计一位病人的体温变化图，这位病人中午12时的体温约为（）

A、39.0℃ B、38.2℃ C、38.5℃ D、37.8℃

查看试题解析
6. 下列各式的变形中，属于因式分解的是（）

A、 $(x + 1) (x - 3) = x^{2} - 2 x - 3$ B、 $x^{2} - y^{2} = (x + y) (x - y)$ C、 $x^{2} - x y - 1 = x (x - y)$ D、 $x^{2} - 2 x + 2 = (x - 1)^{2} + 1$

查看试题解析
7. 如图，点B、F、C、E在一条直线上，∠A＝∠D＝90°，AB=DE，添加下列选项中的条件，能用HL判定△ABC≌△DEF的是（）

A、AC=DF B、∠B=∠E C、∠ACB=∠DFE D、BC=EF

查看试题解析
8. 仔细观察用直尺和圆规作一个角等于已知角的示意图，请根据三角形全等的有关知识，说明画出 $∠ A O B = ∠ C P D$ 的依据是（）

A、 $S A S$ B、 $A A S$ C、 $A S A$ D、 $S S S$

查看试题解析
9. 如图，在4个均由16个小正方形组成的网格正方形中，各有一个格点三角形，那么这4个正方形网格中不是直角三角形的是（）

A、 B、 C、 D、

查看试题解析
10. 如图所示，是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪三条边的距离相等，凉亭的位置应选在（　　）

A、△ABC 的三条中线的交点 B、△ABC 三边的垂直平分线的交点 C、△ABC 三条角平分线的交点 D、△ABC 三条高所在直线的交点

查看试题解析

二、填空题

11. 计算： $a^{7} \div a^{4}$ ＝．

查看试题解析
12. 计算： $2 x^{2} y \cdot (- 3 x y)$ ＝．

查看试题解析
13. “同旁内角互补，两直线平行”的逆命题是.

查看试题解析
14. 计算 $(9 x^{4} - 15 x^{2} + 6 x) \div 3 x =$ ．

查看试题解析
15. 已知x＋2y＝5，x²－4y²＝－15，则2x－4y的值为．

查看试题解析
16. 如图，△ABC中，AB＝AC，点D为BC的中点，∠BAD＝24°，AD＝AE，∠EDC＝度．

查看试题解析
17. 如图，已知 $R t Δ A B C$ 的三边长分别为6、8、10，分别以它们的三边作为直径向外作三个半圆，则图中阴影部分的面积为．

查看试题解析
18. 如图，在△ABC中，∠ABC的角平分线和∠ACB相邻的外角平分线CD交于点D，过点D作DE∥BC交AB于E，交AC于G，若EG=2，且GC=6，则BE长为．

查看试题解析

三、解答题

19. 计算： $\sqrt{(- 4)^{2}}$ － $\sqrt[{}_{3}]{- 8}$ ＋ $\sqrt{1 \frac{9}{16}}$ ．

查看试题解析
20. 化简： ${(a - b)}^{2} + (a + b) (a - b) - {(2 a)}^{2}$ ．

查看试题解析
21. 如图，已知△ABC是等边三角形，点D、E分别在BC、AC边上，且BD＝CE．求证：AD＝BE

查看试题解析
22. 解答

(1)、如图，请计算图形中阴影部分的面积（要求用含x的代数式表示，并化简）

(2)、求当x＝4时，图中阴影部分的面积．

查看试题解析
23. 为了提高学生的阅读能力，我区某校开展了“读好书，助成长”的活动，并计划购置一批图书，购书前，对学生喜欢阅读的图书类型进行了抽样调查，并将调查数据绘制成两幅不完整的统计图，如图所示，请根据统计图回答下列问题：

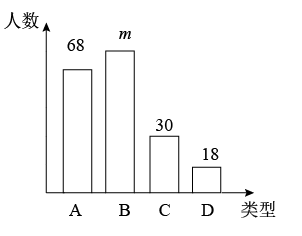
(1)、本次调查共抽取了名学生．

(2)、两幅统计图中的m＝， n＝．

(3)、求扇形统计图中D所在扇形的圆心角度数．

查看试题解析
24. 如图，正方形网格中的每个小正方形边长都是1，每个小正方形的顶点叫做格点，网格中的A和B两点均在格点上，以线段AB为边画等腰三角形ABC，且点C也在格点上．要求如下：

(1)、图中，AC和BC边的长都为有理数．

(2)、图中，AC和BC边中只有一边长为有理数．

查看试题解析
25. 如图，等腰直角三角板如图放置．直角顶点B在直线CD上，分别过点A、E作AC⊥直线CD于点C，ED⊥直线CD于点D．

(1)、求证：CD＝AC + ED．

(2)、若设△ABC三边长分别为a、b、c，利用此图证明勾股定理．

查看试题解析
26. 下面是某同学对多项式（x²－3x+4）（x²－3x+6）+1进行因式分解的过程．
解：设x²－3x＝m
原式＝（m+4）（m+6）+1（第一步）
＝ m²+10m+25（第二步）
＝（m+5）²（第三步）
＝（x²－3x+5）²（第四步）
回答下列问题：

(1)、该同学第二步到第三步运用了因式分解的____．

A、提取公因式 B、平方差公式 C、完全平方公式

(2)、请你模仿以上方法尝试对多项式（x²＋2x）（x²＋2x+6）+9进行因式分解．

(3)、因式分解：（x²－4x＋6）（x²－4x＋2）＋4=（在横线处直接写出因式分解的结果）．

查看试题解析
27. 如图，△ABC中，∠ABC＝90°，AB＝6，BC＝8，AD平分∠BAC，交BC于点D．动点Q从点B出发，按BC—CA的折线路径，以每秒1个单位长度的速度运动，设运动时间为t秒．

(1)、当点Q在AC边上运动时，线段AQ长为（用含t的代数式表示）

(2)、当点Q在AC边上运动时，线段BQ长度不可能是．（填序号即可）
①7.2 ②5.3 ③4.8 ④4.5

(3)、求△ADC的面积．

(4)、当△ABQ为轴对称图形时，请直接写出t的值．

查看试题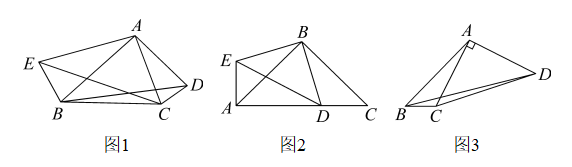解析
28. 解答

(1)、【问题探究】
如图1，锐角△ABC中分别以AB、AC为边向外作等腰△ABE和等腰△ACD，使AE=AB，AC＝AD，∠ABE＝∠ADC，连接EC，BD．求证：EC＝BD．

(2)、【拓展延伸】
①如图2，△ABC中，∠ABC＝90°，CB＝AB，D为AC上一点，连结BD，作BE⊥BD，AE⊥AC，连结DE．若AC＝2，请直接写出四边形ADBE的面积．
②如图3，四边形ABCD中，AD⊥AC，AC＝AD，∠ABC＝45°，AB＝3，BC＝1，请直接写出BD长．

查看试题解析