吉林省长春市南关区2021-2022学年八年级上学期期末数学试题2
试卷更新日期：2022-10-09 类型：期末考试
一、单选题
-
1. 8的立方根是( )A、2 B、－2 C、±2 D、22. 在1，﹣2.8，0，四个实数中，大于1的实数是（ ）A、1 B、﹣2.8 C、0 D、3. 计算（﹣a2）3÷a3结果是（ ）A、﹣a2 B、a2 C、﹣a3 D、a34. 下列说法正确的是（ ）A、命题一定有逆命题 B、所有的定理一定有逆定理 C、真命题的逆命题一定是真命题 D、假命题的逆命题一定是假命题5. 如图，在△ABC中，∠C＝90°，使点P到AB、BC的距离相等，则符合要求的作图痕迹（ ）A、
B、
C、
D、
6. 某年1～4月我国新能源乘用车的月销量情况如图所示，则下列说法错误的是（ ）
A、1月份销量为2.1万辆 B、1～4月新能源乘用车销量逐月增加 C、4月份销量比了3月份增加了1万辆 D、从2月到3月的月销量增长最快7. 如图，所有阴影部分四边形都是正方形，所有三角形都是直角三角形，若正方形A、B、D的面积依次为6、10、24，则正方形C的面积为（ ）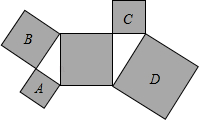
A、4 B、6 C、8 D、128. 如图，在△ABC中，∠BAC=120°，将△ABC绕点C逆时针旋转得到△DEC，点A、B的对应点分别为D、E，连结AD．当A、D、E三点在同一条直线上时，下列结论错误的是（ ）
A、AD＝AC B、∠ABC＝∠ADC C、AB+CD＝AE D、AB∥CD二、填空题
-
9. 立方等于它本身的数有 ．10. 计算：（﹣2x3y）•5xy3＝ ．11. 因式分解： .12. 一个等腰三角形的两边长分别为4cm和8cm，则周长是 cm．13. 如图，在△ABC中，∠B=30°，∠C=50°，通过观察尺规作图的痕迹，∠DAE的度数是 ．
14. 如图，△ABC纸片的面积为12cm2 ， 其中一边BC的长为6cm，将其经过两刀裁剪，拼成了一个无缝隙无重叠的长方形BCDE，则长方形的周长为cm.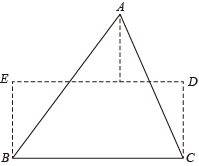
三、解答题
-
15. 计算：（2m2﹣m）2÷（﹣m2）．16. 计算：（2x+5y）（3x﹣2y）．17. 先化简，再求值：2（a+1）（a﹣1）﹣a（2a﹣3），其中a= ．18. 如图，在△ABC中，AB=AC，D是BC边上的中点，∠B=25°．
(1)、求∠DAC的大小．(2)、若AB=13，AD=5，求BC的长．19. 图①、图②均是6×6的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点，点A、B、C均在格点上，只用无刻度的直尺，分别在给定的网格中找一格点P，按下列要求作图．
(1)、在图①中，连结PA、PB，使PA=PB．(2)、在图②中，连结PA、PB、PC，使PA=PB=PC．20. 如图，CD∥AB，CD=CB，点E在BC上，∠D=∠ACB．
(1)、求证：CE＝AB．(2)、若∠A＝125°，则∠BED的度数是 ．21. 某校数学兴趣小组为了解学生对A：新闻、B：体育、C：动画、D：娱乐、E：戏曲五类电视节目的喜爱情况，学校随机抽取了n名学生进行调查，规定每人必须并且只能在以上给出的五类中选择一类节目类型
人数
A
20
B
a
C
52
D
80
E
b
请根据图中所给出的信息解答下列问题：
(1)、n＝ ， a＝ ， b＝ ．(2)、在扇形统计图中，求节目类型“C”所占的百分数．(3)、在扇形统计图中，求节目类型“D”所对应的扇形圆心角的度数．22. 如图，在笔直的公路AB旁有一座山，为方便运输货物现要从公路AB上的D处开凿隧道修通一条公路到C处，已知点C与公路上的停靠站A的距离为15km，与公路上另一停靠站B的距离为20km，停靠站A、B之间的距离为25km，且CD⊥AB．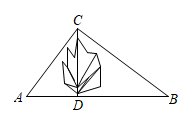
(1)、求修建的公路CD的长；(2)、若公路CD修通后，一辆货车从C处经过D点到B处的路程是多少？23. 操作：第一步：如图1，对折长方形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开．
第二步：如图2，再一次折叠纸片，使点A落在EF上的N处，并使折痕经过点B，得到折痕BM，同时得到线段BN．
(1)、连结AN，易知△ABN的形状是 ．(2)、论证：如图3，若延长MN交BC于点P，试判定△BMP的形状，请说明理由．24. 教材呈现：如图是华师版八年级上册数学教材第94页的部分内容．
(1)、请根据所给教材内容，结合图①，写出“线段垂直平分线的性质定理”完整的证明过程．
(2)、定理应用：如图②，在△ABC中，AB、AC的垂直平分线分别交BC于点D、E，垂足分别为M，N，已知△ADE的周长为22，则BC的长为 ．
(3)、如图③，在△ABC中，AB=AC，AD⊥BC，E、P分别是AB、AD上任意一点，若BC=6，AB=5，则BP+EP的最小值是 ．25. 如图，在△ABC中，CA＝CB，点M、N分别在边BC、AC上（点M、N不与所在线段端点重合），且BM＝AN，连结MA并延长交AD的垂直平分线于点E，连结ED．
(1)、【猜想】如图①，当∠C＝30°时，可证△BCN≌△ACM，进而得出∠BDE的大小为 度．(2)、【探究】如图②，若∠C＝β．①求证：△BCN≌△ACM．
②∠BDE的大小为 ▲ 度（用含β的代数式表示）．
(3)、【应用】如图③，当∠C＝120°时，AM平分∠BAC，DE＝DF，则△DEF的面积为 ．