吉林省长春市绿园区2021-2022学年八年级上学期期末数学试题2
试卷更新日期:2022-10-09 类型:期末考试
一、单选题
-
1. -8的立方根是( )A、4 B、±2 C、2 D、
-
2. 下列数是无理数的是( )A、 B、π C、0 D、
-
3. 计算的结果是( )A、 B、 C、 D、
-
4. 计算 的结果为( )A、 B、 C、 D、
-
5. 计算(4+x)(x-4)的结果是( )A、 B、 C、 D、
-
6. 如图所示,在中, , 分别以AB、BC、AC为边向外作正方形,面积分别为225、400、S,则S为( )
 A、625 B、600 C、175 D、25
A、625 B、600 C、175 D、25 -
7.
如图所示,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=28°,则∠AEC=( )
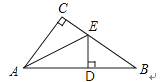 A、28° B、59° C、60° D、62°
A、28° B、59° C、60° D、62° -
8. 在△ABC中,∠BAC=90°,AB>AC,∠B≠30°,用无刻度的直尺和圆规在BC边上找一点D,使AD=BD,下列作法正确的是( )A、
 B、
B、 C、
C、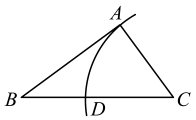 D、
D、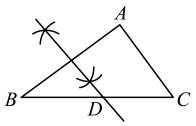
二、填空题
-
9. 二次根式有意义,则的取值范围是
-
10. 比较大小: .0(填“>”、“=”或“<”).
-
11. 计算:2x•(﹣3xy)= .
-
12. 若一个三角形的三边长分别为5、12、13,则此三角形的面积为 .
-
13. 如图,在△ABC中,∠C=90°,AD平分∠BAC,AB=5,CD=2,则△ABD的面积是 .

-
14. 如图,在△ABC中,AB=AC,D为边BC上一点,且∠BAD=30°,若AD=DE,∠DAE=72°,则∠EDC的度数为°.

三、解答题
-
15. 计算: .
-
16. 因式分解:(1)、;(2)、
-
17. 图①、图②均是4×4的正方形网格,每个小正方形的顶点称为格点,小正方形的边长均为1,点A、点B均在格点上,在给定的网格中按要求画图,所画图形的顶点均在格点上.
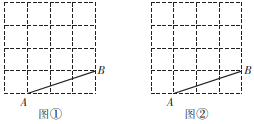 (1)、在图①中,以线段AB为腰画一个等腰三角形.(2)、在图②中,以线段AB为底画一个等腰三角形.
(1)、在图①中,以线段AB为腰画一个等腰三角形.(2)、在图②中,以线段AB为底画一个等腰三角形. -
18. 先化简,再求值: , 其中
-
19. 如图,点B、F、C、E四点在同一条直线上, , , . 求证: .

-
20. 如图,甲乙两船从港口A同时出发,甲船以16海里/时速度沿北偏东方向航行,乙船沿南偏东方向航行,3小时后,甲船到达C岛,乙船到达B岛.若C、B两岛相距60海里,问:乙船的航速是多少?

-
21. 图(1)是一个长为 , 宽为的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形.
 (1)、图2中间空白的部分的面积是 ;(2)、观察图2,请你写出代数式、、之间的等量关系式 ;(3)、根据你得到的关系式解答下列问题:若 , , 求的值.
(1)、图2中间空白的部分的面积是 ;(2)、观察图2,请你写出代数式、、之间的等量关系式 ;(3)、根据你得到的关系式解答下列问题:若 , , 求的值. -
22. 2021年央视春晚,数十个节目给千家万户送上了丰富的“年夜大餐”.某校随机对八年级部分学生进行了一次调查,对最喜欢相声《年三十的歌》(记为A)、歌曲《牛起来》(记为B)、武术表演《天地英雄》(记为C)、小品《开往春天的幸福》记为D)的同学进行了统计(每位同学只选择一个最喜欢的节目),绘制了以下不完整的统计图,请根据图中信息解答问题:
 (1)、求本次接受调查的学生人数.(2)、求扇形统计图中D所在扇形的圆心角度数(3)、将条形统计图补充完整.
(1)、求本次接受调查的学生人数.(2)、求扇形统计图中D所在扇形的圆心角度数(3)、将条形统计图补充完整. -
23. 在中, , , 直线MN经过点C且于D,于E.
 (1)、当直线MN绕点C旋转到图1的位置时,求证:
(1)、当直线MN绕点C旋转到图1的位置时,求证:①≌;
②;
(2)、当直线MN烧点C旋转到图2的位置时,求证:;(3)、当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明. -
24. 如图,在中, , , , 点D是边的中点,动点P从点D出发,沿以每秒2个单位长度的速度向终点A匀速运动.同时,动点Q从点D出发,沿以每秒1个单位长度的速度向终点C匀速运动.当点P到达终点时,点Q也随之停止运动.过点Q作 , 使 , 且点E落在直线的上方,当点P不与点D重合时,以、为邻边作长方形 . 设长方形与的重叠部分的面积为S,点P的运动时间为t(秒 .
 (1)、用含t的代数式表示线段的长度为 .(2)、当点F落在线段上时,求t的值.(3)、用含t的代数式表示S.(4)、连接、 . 当是等腰三角形时,直接写出t的值.
(1)、用含t的代数式表示线段的长度为 .(2)、当点F落在线段上时,求t的值.(3)、用含t的代数式表示S.(4)、连接、 . 当是等腰三角形时,直接写出t的值.
