吉林省长春市净月高新区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中，无理数的是（）

A、 $0$ B、 $- \frac{1}{2}$ C、 $\sqrt{2}$ D、 $\frac{22}{7}$

查看试题解析
2. 计算 $a^{6} \div a^{3}$ ，正确的结果是（）

A、 $3$ B、 $a^{3}$ C、 $a^{2}$ D、 $3 a$

查看试题解析
3. 实数16的算术平方根是（　　）

A、8 B、±8 C、4 D、±4

查看试题解析
4. 为配合全科大阅读活动，学校团委对全校学生阅读兴趣调查的数据进行整理．欲反映学生感兴趣的各类图书所占百分比，最适合的统计图是（）

A、条形统计图 B、频数直方图 C、折线统计图 D、扇形统计图

查看试题解析
5. 已知 $y^{2} - 6 y + m$ 是完全平方式，则m=（）

A、 $6$ B、 $- 6$ C、 $9$ D、 $- 9$

查看试题解析
6. 汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝．如图所示的弦图中，四个直角三角形都是全等的，它们的斜边长为5，较短直角边长为3，则图中小正方形（空白区域）的面积为（）

A、1 B、4 C、6 D、9

查看试题解析
7. 如图，在 $△$ ABC中，AD平分∠BAC ， $D E // A C$ ，AB=7cm，BD=3cm，则 $△$ BDE的周长为（）

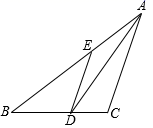A、13cm B、10cm C、4cm D、7cm

查看试题解析
8. 如图，在边长分别为a，b的两个正方形组成的图形中，剪去一个边长为（a-b）的正方形，通过用两种不同的方法计算剪去的正方形的面积，可以验证的乘法公式是（）

A、 $a (a + b) = a^{2} + a b$ B、 $(a + b) (a - b) = a^{2} - b^{2}$ C、 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ D、 $(a - b)^{2} = a^{2} - 2 a b + b^{2}$

查看试题解析

二、填空题

9. -64的立方根是。

查看试题解析
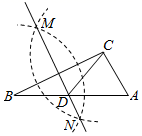
10. 因式分解： $a^{3} - 4 a =$ ．

查看试题解析
11. 命题“线段垂直平分线上的任意一点，到这条线段两个端点距离相等”的逆命题是．

查看试题解析
12. 计算： $(14 a^{3} - 7 a) \div (7 a) =$ .

查看试题解析
13. 如图是按以下步骤作图：（1）在△ABC中，分别以点B ， C为圆心，大于 $\frac{1}{2}$ BC长为半径作弧，两弧相交于点M ， N；（2）作直线MN交AB于点D；（3）连接CD ，若∠BCA＝90°，AB＝6，则CD的长为．

查看试题解析
14. 如图，在 $△ A B C$ 中， $B D$ 平分 $∠ A B C$ ，如果 $A B = 8$ ， $B C = 12$ ， $△ A B D$ 的面积为 $16$ ，则 $△ C B D$ 的面积为．

查看试题解析

三、解答题

15. 计算：

(1)、 $\sqrt{12} - \sqrt[3]{- 8} + \sqrt{3}$ ；

(2)、 $(m - 2 n) (2 m + n)$ ．

查看试题解析
16. 先化简，再求值 $2 (a^{2} - 5) - (a + 1) (a - 1)$ ，其中 $a = \sqrt{3}$ ．

查看试题解析
17. 已知：如图，AB＝DE，AC＝DF，BE＝CF．求证：∠A＝∠D．

查看试题解析
18. 如图，在等边△ABC中，点D ， E分别在边BC ， AC上，DE∥AB ，过点E作EF⊥DE ，交BC的延长线于点F ．

(1)、求∠F的度数；

(2)、求证：DC＝CF ．

查看试题解析
19. 图①、图②都是 $4 \times 4$ 的正方形网格，每个小正方形的边长均为 $1$ ，每个小正方形的顶点叫做格点，线段 $A B$ 的端点都在格点上．在给定的网格中，只用无刻度的直尺，在图①、图②中，按下列要求画图，所画的图形的顶点均在格点上．

(1)、在图①中画一个以 $A B$ 为腰的等腰三角形 $A B C$ ；

(2)、在图②中画一个以 $A B$ 为底边的等腰三角形 $A B D$ ．

查看试题解析
20. 伊通河，是长春平原上的千年古流，是松花江的二级支流，它发源于吉林省伊通县境内哈达岭山脉青顶山北麓，如图，在伊通河笔直的河流一侧有一旅游地 $C$ ，河边有两个景点 $A$ 、 $B ．$ 其中 $A B = A C$ ，由于某种原因，由 $C$ 到 $A$ 的路现在已经不通，为方便游客决定在河边新建一个景点H（ $A$ 、 $H$ 、 $B$ 三点在同一直线上），并新修一条路 $C H$ ，测得 $B C = 5$ 千米， $C H = 4$ 千米， $B H = 3$ 千米．

(1)、判断 $Δ B C H$ 的形状，并说明理由；

(2)、求原路线 $A C$ 的长．

查看试题解析
21. 近年来，国家对中小学劳动教育越来越重视，净月高新区响应号召成立劳动实践教育基地，为了解学生对劳动知识的掌握情况，劳动基地教师随机抽取了区内某所学校n名学生进行问卷调查，将他们的得分按优秀、良好、合格、待合格四个等级进行统计，并绘制了不完整的统计表和条形统计图：
$n$ 名学生掌握劳动知识统计表：
等级
频数
频率
优秀
$28$
$0.56$
良好
a
$0.3$
合格
$5$
b
待合格
$2$
$0.04$

(1)、n的值为， a的值为， b的值为；

(2)、补全条形统计图；

(3)、若全校有3000名学生，请估计该校掌握劳动知识达到“优秀”和“良好”等级的学生有多少人．

查看试题解析
22. 【教材呈现】如图是华师版八年级上册数学教材第117页的部分内容．

把两个全等的直角三角形拼成如图所示的形状，使点 $A$ 、 $E$ 、 $D$ 在同一条直线上，利用此图的面积表示式证明勾股定理．

(1)、请结合图①，写出完整的证明过程；

(2)、如图②，等腰直角三角形ABC，∠BAC=90°，AB=2 $\sqrt{2}$ ， P是射线BC上一点，以AP为直角边在AP边的右侧作△APD，使∠APD=90°，AP=PD．过点D，作DE⊥BC于点E，当DE=4时，则BD= ．

查看试题解析
23. 如图，△ABC和△DCE都是等边三角形．

(1)、探究发现
△BCD与△ACE是否全等？若全等，加以证明；若不全等，请说明理由；

(2)、拓展运用
若B、C、E三点不在一条直线上，∠ADC=30°，AD=3，CD=2，求BD的长；

(3)、若△DCE绕点C旋转，△ABC和△DCE的边长分别为1和2，当△BCD的面积最大时，AE的长为．

查看试题解析
24. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A B = 5$ ， $B C = 3$ ，点P从点A出发，以每秒2个单位长度的速度沿折线 $A - C - B - A$ 运动．设点P的运动时间为t秒 $(t > 0)$ ．

(1)、求AC的长及斜边AB上的高．

(2)、当点P在CB上时，
①CP的长为（用含t的代数式表示）．

②若点P在 $∠ B A C$ 的角平分线上，则t的值为．

(3)、在整个运动过程中，直接写出 $△ B C P$ 是等腰三角形时t的值．

查看试题解析

等级	频数	频率
优秀	$28$	$0.56$
良好	a	$0.3$
合格	$5$	b
待合格	$2$	$0.04$