吉林省长春市2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 4的平方根是（）

A、2 B、﹣2 C、±2 D、没有平方根

查看试题解析
2. 计算 $m^{6} \div m^{2}$ 的结果是（）

A、 $m^{3}$ B、 $m^{4}$ C、 $m^{8}$ D、 $m^{12}$

查看试题解析
3. 数字“20211202”中，数字“2”出现的频数是（）

A、1 B、2 C、3 D、4

查看试题解析
4. 下列命题中是假命题的是（）

A、两点之间，线段最短 B、同旁内角互补 C、等角的补角相等 D、垂线段最短

查看试题解析
5. 在 $△ A B C$ 中，若 $A C^{2} - B C^{2} = A B^{2}$ ，则（）

A、 $∠ A = 90 °$ B、 $∠ B = 90 °$ C、 $∠ C = 90 °$ D、不能确定

查看试题解析
6. 打碎的一块三角形玻璃如图所示，现在要去玻璃店配一块完全一样的玻璃，最省事的方法是（）

A、带①②去 B、带②③去 C、带③④去 D、带②④去

查看试题解析
7. 如图，在Rt△ABC中，∠C＝90°，以顶点A为圆心，适当长为半径画圆弧，分别交AB、AC于点D、E，再分别以点D、E为圆心，大于 $\frac{1}{2}$ DE长为半径画圆弧，两弧交于点F，作射线AF交边BC于点G．若CG＝3，AB＝10，则△ABG的面积是（）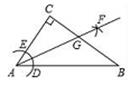

A、3 B、10 C、15 D、30

查看试题解析
8. 若 $△ A B C$ 中刚好有 $∠ B = 2 ∠ C$ ，则称此三角形为“可爱三角形”，并且 $∠ A$ 称作“可爱角”．现有一个“可爱且等腰的三角形”，那么聪明的同学们知道这个三角形的“可爱角”应该是（）．

A、 $45 °$ 或 $36 °$ B、 $7 2^{∘}$ 或 $3 6^{∘}$ C、 $45 °$ 或 $72 °$ D、 $36 °$ 或 $72 °$ 或 $45 °$

查看试题解析

二、填空题

9. 比较大小： $\sqrt{17}$ 5．（填“>”或“<”或“=”）

查看试题解析
10. 因式分解： $a^{3} - 4 a =$ ．

查看试题解析
11. 如图，在△ABC中，AB＝AC，边AB的垂直平分线DE交BC于点E，连结AE，若∠BAC＝120°，则∠AEC的大小为度．

查看试题解析
12. 已知长方形面积为6y⁴﹣3x²y³+x²y² ，它的一边长为3y² ，则这个长方形另外一边长为．

查看试题解析
13. 如图，已知△ABC是等边三角形，点B、C、D、E在同一直线上，且CG=CD，DF=DE，则∠E=度．

查看试题解析
14. 如图，Rt△ABC中，AB $= \frac{9}{2}$ ， BC＝3，∠B＝90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为．

查看试题解析

三、解答题

15. 计算： ${(- 2)}^{2} + | \sqrt{2} - 1 | - \sqrt{9} + \sqrt[3]{- 8}$ ．

查看试题解析
16. 计算： $3 x^{2} y^{2} \cdot {(- 2 x y^{2} z)}^{2}$ ．

查看试题解析
17. 先化简，再求值： $(x + 1) (x - 1) - {(x - 2)}^{2}$ ，其中 $x = 3$ ．

查看试题解析
18. 如图，△ABC中，AB＝AC，点E、F在边BC上，BF＝CE，求证：AE＝AF．

查看试题解析
19. 图①、图②都是4×4的正方形网格，每个小正方形的顶点为格点，每个小正方形的边长均为1，在图①、图②中已画出AB，点A、B均在格点上，按下列要求画图：

(1)、在图①中，画一个以AB为腰且三边长都是无理数的等腰三角形ABC，点C为格点；

(2)、在图②中，画一个以AB为底的等腰三角形ABD，点D为格点．

查看试题解析
20. 为了解某校学生睡眠时间情况，随机抽取若干学生进行调查．学生睡眠时长记为x小时，将所得数据分为5组（A： $x \geq 10$ ；B： $9 \leq x < 10$ ；C： $8 \leq x < 9$ ；D： $7 \leq x < 8$ ；E： $x < 7$ ），学校将所得到的数据进行分析，得到如下部分信息：
请你根据以上信息，回答下列问题：

(1)、直接写出a的值；

(2)、补全条形统计图；

(3)、根据学校五项管理有关要求，中学生睡眠时间应不少于9个小时，那么估计该中学1000名学生中符合要求的有多少人？

查看试题解析
21. 如图，在笔直的公路AB旁有一座山，为方便运输货物现要从公路AB上的D处开凿隧道通一条公路到C处，已知点C与公路上的停靠站A的距离为3km，与公路上另一停靠站B的距离为4km，且AC⊥BC，CD⊥AB．

(1)、求修建的公路CD的长；

(2)、若公路CD建成后，一辆货车由C处途经D处到达B处的总路程是多少km？

查看试题解析
22. 如图1，在一个平面直角三角形中的两直角边的平方之和一定等于斜边的平方。在△ABC中，∠C=90°，则AC²+BC²＝AB² ．我们定义为“商高定理”。

(1)、如图1，在△ABC中，∠C=90°中，BC＝4，AB＝5，试求AC＝；

(2)、如图2，四边形ABCD的对角线AC、BD交于点O，AC⊥BD．试证明：AB²+CD²＝AD²+BC²；

(3)、如图3，分别以Rt△ACB的直角边BC和斜边AB为边向外作正方形BCFG和正方形ABED，连结CE、AG、GE．已知BC＝4，AB＝5，求GE²的值．

查看试题解析
23.

(1)、【知识生成】用两种不同方法计算同一图形的面积，可以得到一个等式，如图1，是用长为x，宽为y（x＞y）的四个全等长方形拼成一个大正方形，用两种不同的方法计算阴影部分（小正方形）的面积，可以得到（x﹣y）²、（x+y）²、xy三者之间的等量关系式：；

(2)、【知识迁移】如图2所示的大正方体是由若干个小正方体和长方体拼成的，用两种不同的方法计算大正方体的体积，我们也可以得到一个等式：；

(3)、【成果运用】利用上面所得的结论解答：
①已知x＞y，x+y＝3，xy $= \frac{5}{4}$ ，求x﹣y的值；

②已知|a+b﹣4|+（ab﹣2）²＝0，则a³+b³＝　 ▲ 　．

查看试题解析
24. 如图，在△ABC中，AB＝AC＝18cm，BC＝10cm，AD＝2BD．动点P以2cm/s的速度沿射线BC运动，同时，点Q从点C出发，以acm/s的速度向终点A运动，当Q点停止运动时，P点也随之停止运动，设点P的运动时间为t（s）（t＞0）．

(1)、用含t的代数式表示PC的长；

(2)、若点Q的运动速度为1cm/s，当△CQP是以∠C为顶角的等腰三角形时，求t的值；

(3)、当点Q的运动速度为多少时，能使△BPD与△CQP在某一时刻全等．

查看试题解析