吉林省四平市铁东区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $b^{3} \cdot b^{3} = 2 b^{3}$ B、 $b^{3} \cdot b^{3} = b^{9}$ C、 $b^{3} \div b^{3} = b$ D、 $b \cdot b^{- 1} = 1$

查看试题解析
2. 已知三角形两边的长分别是3和7，则此三角形第三边的长可能是（）

A、1 B、2 C、8 D、11

查看试题解析
3. 已知 $\frac{1}{a} - \frac{1}{b} = \frac{1}{2}$ ，则 $\frac{a b}{a - b}$ 的值是（）

A、 $\frac{1}{2}$ B、- $\frac{1}{2}$ C、2 D、-2

查看试题解析
4. 如图，在△ABC中，AB=AC，AD=DB，DE⊥AB于点E，若BC=3，且△BDC的周长为7，则AE的长为（）

A、2 B、2.5 C、3 D、3.5

查看试题解析
5. 如果一个多边形的内角和是其外角和的3倍，那么，从这个多边形的一个顶点出发画对角线，一共能画出对角线的条数为（）

A、4 B、5 C、6 D、7

查看试题解析
6. 如图，OP平分∠AOB，PA⊥OA，PB⊥OB，垂足分别为A、B，下列四个结论正确的个数是（）
①PA=PB ②PO平分∠APB ③OA=OB ④OP垂直平分AB．

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

7. 纳米（nm）也叫毫微米，是非常小的长度单位，15nm＝0.000000015m用科学记数法表示数0.000000015为．

查看试题解析
8. 分式 $\frac{x + 1}{x (x - 1)}$ 中隐含着x的取值应该满足的条件是：．

查看试题解析
9. 因式分解： $(x - y)^{2} + 4 x y =$ ．

查看试题解析
10. 如图，D、E、F分别为BC、AD、CE的中点．若S_△ABC=8cm² ，则S_△DEF= ．

查看试题解析
11. 等腰三角形的一个内角是 $80^{°}$ ，则它的顶角度数是．

查看试题解析
12. 如图，在△ABC中，按以下步骤作图：①分别以A、B为圆心，大于 $\frac{1}{2}$ AB的长为半径画弧，两弧相交于M、N两点；②作直线MN交BC于点D．若AD=AC，∠B=25°，则∠BAC= ．

查看试题解析
13. 如图，Rt△ABC中，∠ACB=90°，将其折叠，使点A落在边CB上 $A^{'}$ 处，折痕为CD．若AB=10，BC=8，AC=6，则 $△ A^{'} D B$ 的周长为．

查看试题解析
14. 如图，等边三角形ABC的边长为4，AD是BC边上的中线，F是AD边上的动点，E是边AC的中点．当△ECF的周长取得最小值时，∠EFC的度数为．

查看试题解析

三、解答题

15. 计算： $(x - y) (x^{2} + x y + y^{2})$ .

查看试题解析
16. 解方程： $\frac{2}{x - 1} = \frac{4}{x^{2} - 1}$ ．

查看试题解析
17. 作图并填空

(1)、请在直角坐标系中画出与△ABC关于y轴对称的△A₁B₁C₁；

(2)、点A₁的坐标是：．
点B₁的坐标是：．
点C₁的坐标是：．

查看试题解析
18. 如图，AB=DE，AC=DF，BE=CF．求证：AC∥DF．

查看试题解析
19. 先化简，再求值： $(m + 2 + \frac{5}{2 - m}) \div \frac{3 - m}{2 m - 4}$ ，其中 $m = - \frac{1}{2}$ ．

查看试题解析
20. 已知，如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高。求证：AD垂直平分EF。

查看试题解析
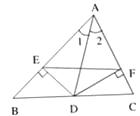21. 如图，在方格纸中，△PQR的三个顶点及A，B，C，D，E五个点都在小方格的顶点上，请以A，B，C，D，E中的三个点为顶点画三角形：

(1)、在图甲中画出一个三角形，使之与△PQR全等；

(2)、在图乙中画出一个三角形，使之与△PQR面积相等但不全等．

(3)、直接写出△PQR的面积等于．

查看试题解析
22. 如图，∠AOB=60°，OC平分∠AOB，过点C作CD⊥OC，交OB于点D， $C E ∥ O A$ ，交OB于点E．

(1)、若OD=7，求CD的长；

(2)、试判定△ECD的形状．

查看试题解析
23. 如图，已知BN平分∠ABC，P为BN上的一点，PF⊥BC于F，PA=PC．

(1)、求证：∠PCB+∠BAP=180°；

(2)、线段BF、BC、AB之间有怎样的数量关系？请直接写出你探究的结论：．

查看试题解析
24. 第二实验中学八年级学生去距学校10千米的文化广场参加活动，一部分同学骑自行车先走，过了25分钟后，其余同学乘汽车出发，结果他们同时到达．已知汽车的平均速度是骑车同学平均速度的2倍，求汽车的平均速度．

查看试题解析
25. 已知：在 $Δ A B C$ 中， $A C = B C$ ， $∠ A C B = 90 °$ ，过点C作 $C D ⊥ A B$ 于点D，点E是 $A B$ 边上一动点（不含端点A、B），连接 $C E$ ，过点B作 $C E$ 的垂线交直线 $C E$ 于点F，交直线 $C D$ 于点G（如图①）.

(1)、求证： $A E = C G$ ；

(2)、若点E运动到线段 $B D$ 上时（如图②），试猜想 $A E$ 、 $C G$ 的数量关系是否发生变化，请直接写出你的结论；

(3)、过点A作 $A H$ 垂直于直线 $C E$ ，垂足为点H，并交 $C D$ 的延长线于点M（如图③），找出图中与 $B E$ 相等的线段，并证明.

查看试题解析
26. 如图（1），AB＝4 $c m$ ，AC⊥AB，BD⊥AB，AC＝BD＝3 $c m$ .点 P 在线段 AB 上以 1 $c m / s$ 的速度由点 A 向点 B 运动，同时，点 Q 在线段 BD 上由点 B 向点 D 运动.它们运动的时间为 t（s）.

(1)、若点 Q 的运动速度与点 P 的运动速度相等，当 $t$ ＝1 时，△ACP 与△BPQ 是否全等，请说明理由，并判断此时线段 PC 和线段 PQ 的位置关系；

(2)、如图（2），将图（1）中的“AC⊥AB，BD⊥AB”为改“∠CAB＝∠DBA＝60°”，其他条件不变.设点 Q 的运动速度为 $x$ $c m / s$ ，是否存在实数x，使得△ACP 与△BPQ 全等？若存在，求出相应的x、t的值；若不存在，请说明理由.

查看试题解析