黑龙江省绥化市北林区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 在函数y= $\sqrt{x + 3}$ 中，自变量x的取值范围是（）

A、x≤﹣3 B、x≥﹣3 C、x＜﹣3 D、x＞﹣3

查看试题解析
2. 若一次函数 $y = (k - 2) x + 1$ 的函数值 $y$ 随 $x$ 的增大而增大，则（）

A、 $k < 2$ B、 $k > 2$ C、 $k > 0$ D、 $k < 0$

查看试题解析
3. 下列等式一定成立的是（）

A、 $\sqrt{9} - \sqrt{4} = \sqrt{5}$ B、 $\sqrt{5} \times \sqrt{3} = \sqrt{15}$ C、 $\sqrt{9} = \pm 3$ D、 $- \sqrt{{(- 3)}^{2}} = 3$

查看试题解析
4. 已知四边形ABCD是平行四边形，下列结论中错误的是（）

A、当∠ABC=90°时，它是矩形 B、当AB=BC时，它是菱形 C、当AC⊥BD时，它是菱形 D、当AC=BD时，它是正方形

查看试题解析
5. 在 $R t △ A B C$ 中，斜边 $B C = 5$ ，则 $A B^{2} + A C^{2}$ 等于（）

A、5 B、25 C、50 D、100

查看试题解析
6. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，两直角边 $A C = 6 c m$ ， $B C = 8 c m$ ，现将AC沿AD折叠，使点C落在斜边AB上的点E处，则CD长为（）

A、 $3 c m$ B、 $4 c m$ C、 $5 c m$ D、 $6 c m$

查看试题解析
7. 实数 $a 、 b$ 在数轴上对应点如图所示，则化简 $\sqrt{b^{2}} + \sqrt{{(a - b)}^{2}} - | a |$ 的结果是（）

A、 $2 a$ B、 $2 b$ C、 $- 2 b$ D、 $- 2 a$

查看试题解析
8. 如图，在平行四边形ABCD中，AC、BD相交于点O，点E是CD的中点，若 $O E = 3 c m$ ，则AD的长是（）

A、 $3 c m$ B、 $6 c m$ C、 $9 c m$ D、 $12 c m$

查看试题解析
9. 某校10名学生参加课外实践活动的时间分别为： 3，3，6，4，3，7，5，7，4，9(单位：小时)，这组数据的众数和中位数分别为 ( )

A、9和7 B、3和3 C、3和4.5 D、3和5

查看试题解析
10. 端午节三天假期的某一天，小明全家上午8时自驾小汽车从家里出发，到某著名旅游景点游玩．该小汽车离家的距离S（千米）与时间t（小时）的关系如图所示．根据图象提供的有关信息，下列说法中错误的是（）

A、景点离小明家180千米 B、小明到家的时间为17点 C、返程的速度为60千米每小时 D、10点至14点，汽车匀速行驶

查看试题解析

二、填空题

11. 已知直角三角形的两边长分别为3和4，则斜边上的中线长为．

查看试题解析
12. 如果 $y = \sqrt{x - 2} + \sqrt{2 - x} + 3$ ，那么 $x + y =$ ．

查看试题解析
13. 一次函数 $y = - 2 x + 1$ 不经过第象限．

查看试题解析
14. 如图，在矩形ABCD中，对角线AC、BD相交于点O，若 $∠ A O D = 60 °$ ， $A D = 4$ ，则AB的长为．

查看试题解析
15. 若函数 $y = (2 - m) x^{| m - 1 ∣}$ 是正比例函数，则m= ．

查看试题解析
16. 如图所示，点A的坐标为(2，1)，点B的坐标为(5，3)，点C为x轴上一动点，则AC＋BC的最小值是．

查看试题解析
17. 如图，在菱形ABCD中，过点C作CE⊥BC交对角线BD 于点 E ，若∠ECD=20° ，则∠ADB=.

查看试题解析
18. 如图，直线 $y_{1} = k_{1} x + a$ 与 $y_{2} = k_{2} x + b$ 的交点坐标为(1，2)，则关于x的不等式 $k_{1} x + a < k_{2} x + b$ 的解集为．

查看试题解析
19. 以正方形ABCD的边AD作等边△ADE，则∠BEC的度数是．

查看试题解析
20. 如图如果以正方形 $A B C D$ 的对角线 $A C$ 为边作第二个正方形 $A C E F$ ，再以对角线 $A E$ 为边作第三个正方形 $A E C H$ ，如此下去，…，已知正方形 $A B C D$ 的面积 $S_{1}$ 为1，按上述方法所作的正方形的面积依次为 $S_{2}$ ， $S_{3}$ … $S_{n}$ （ $n$ 为正整数），那么第8个正方形的面积 $S_{8} =$ .

查看试题解析

三、解答题

21. 计算

(1)、 $\frac{\sqrt{27}}{\sqrt{3}} - \sqrt{\frac{1}{2}} \times \sqrt{8} + \sqrt{12}$

(2)、 $(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2}) - {(\sqrt{3} - 1)}^{2}$

查看试题解析
22. 先化简，再求值
$\frac{a^{2} - b^{2}}{a^{2} b - a b^{2}} \div (1 + \frac{a^{2} + b^{2}}{2 a b})$ ，其中 $a = \sqrt{2}$ ， $b = 1$

查看试题解析
23. 某市团委举办“我的中国梦”为主题的知识竞赛，甲、乙两所学校参赛人数相等，比赛结束后，发现学生成绩分别为70分、80分、90分、100分，并根据统计数据绘制了如下不完整的统计图表：
乙校成绩统计表
分数/分
人数/人
70
7
80
90
1
100
8

(1)、在图①中，“80分”所在扇形的圆心角度数为；

(2)、请你将图②补充完整；

(3)、求乙校成绩的平均分；

(4)、经计算知S_甲²＝135，S_乙²＝175，请你根据这两个数据，对甲、乙两校成绩作出合理评价．

查看试题解析
24. 如图，在▱ABCD中，AE⊥BC，AF⊥CD，垂足分别为E，F，且BE=DF．

(1)、求证：▱ABCD是菱形；

(2)、若AB=5，AC=6，求▱ABCD的面积．

查看试题解析
25. 如图所示， $l_{甲}$ 、 $l_{乙}$ 分别表示甲走路与乙骑自行车（按同一路线）行走的路程S（单位：km）与时间t（单位：h）的关系，观察图像回答下列问题：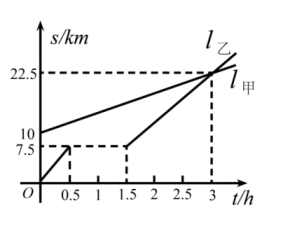

(1)、乙出发时，与甲相距km；

(2)、走了一段路后，乙的自行车发生故障，停下来修理，修车时间为h；

(3)、乙从出发起，经过h与甲相遇；

(4)、求出甲行走的路程S与时间t的函数关系式（写出过程）；

(5)、如果乙的自行车不出故障，那么乙出发后经过h与甲相遇？相遇处乙的出发点km．

查看试题解析
26. 材料阅读
小明偶然发现线段AB的端点A的坐标为 $(1 ， 2)$ ，端点B的坐标为 $(3 ， 4)$ ，则线段AB中点的坐标为 $(2 ， 3)$ ，通过进一步的探究发现在平面直角坐标系中，以任意两点 $P (x_{1} ， y_{1})$ 、 $Q (x_{2} ， y_{2})$ 为端点的线段中点坐标为 $(\frac{x_{1} + x_{2}}{2} ， \frac{y_{1} + y_{2}}{2})$ ．

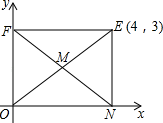(1)、知识运用：
如图，矩形ONEF的对角线相交于点M，ON、OF分别在x轴和y轴上，O为坐标原点，点E的坐标为 $(4 ， 3)$ ，则点M的坐标为．

(2)、能力拓展：
在直角坐标系中，有 $A (- 1 ， 2)$ ， $B (3 ， 1)$ ， $C (1 ， 4)$ 三点，另有一点D与点A、B、C构成平行四边形的顶点，求点D的坐标．

查看试题解析
27. 学习用品超市出售两种笔记本：小笔记本6元/个，大笔记本10元/个，若一次购买大笔记本不超过20个时，按原价出售，购买数量超过20个时，超过的部分打八折出售；购买小笔记本均按原价出售．

(1)、写出购买小笔记本的金额 $y_{1}$ （单位：元）与购买小笔记本的数量x（单位：个）之间的关系式，并直接写出自变量的取值范围；

(2)、写出购买大笔记本的金额 $y_{2}$ （单位：元）与购买大笔记本的数量x（单位：个）之间的关系式，并直接写出自变量的取值范围；

(3)、为了奖励表现突出学生，某学年计划到学习用品超市购买这两种笔记本共90个，其中小笔记本的数量不超过大笔记本数量的一半，两种笔记本各买多少个时，总费用最少，最少费用是多少元？

查看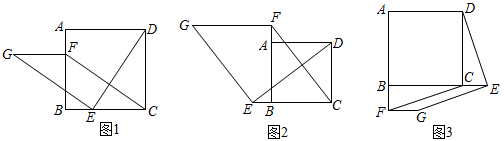试题解析
28.

(1)、问题发现：
如图1，在正方形ABCD中，点E、F分别是边BC、AD上的点，且 $C E = B F$ ，连接DE，过点E作 $E G ⊥ D E$ ，使 $E G = D E$ ，连接FG、FC，请判断：FG与CE的数量关系是，位置关系是．

(2)、拓展探究：
如图2，若点E、F分别是CB、BA延长线上的点，其它条件不变，（1）中结论是否仍然成立？请写出判断，并给予证明．

(3)、类比延伸：
如图3，若点E、F分别是BC、AB延长线上的点，其它条件不变，（1）中结论是否仍然成立？请直接写出你的判断，不需证明．

查看试题解析

分数/分	人数/人
70	7
80
90	1
100	8