黑龙江省齐齐哈尔市铁锋区2021-2022学年八年级上学期期末数学试题2

试卷更新日期：2022-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、 $a^{2} - a = a$ B、 $a x + a y = a x y$ C、 $m^{2} \cdot m^{4} = m^{6}$ D、 ${(y^{3})}^{2} = y^{5}$

查看试题解析
2. 在一些美术字中，有的汉字是轴对称图形．下面4个汉字中，可以看作是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 已知关于x的分式方程 $\frac{m}{x - 1}$ + $\frac{3}{1 - x}$ =1的解是非负数，则m的取值范围是（）

A、m＞2 B、m≥2 C、m≥2且m≠3 D、m＞2且m≠3

查看试题解析
4.
如图，下列条件中，不能证明△ABC≌△DCB的是（　　）

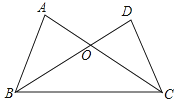A、AB=DC，AC=DB B、AB=DC，∠ABC=∠DCB C、BO=CO，∠A=∠D D、AB=DC，∠DBC=∠ACB

查看试题解析
5. 已知点 $P (3 ， - 2)$ 与点Q关于x轴对称，则Q点的坐标为（　　）

A、 $(- 3 ， 2)$ B、 $(- 3 ， - 2)$ C、 $(3 ， 2)$ D、 $(3 ， - 2)$

查看试题解析
6. 下列说法正确的是（）

A、角平分线上的点到这个角两边的距离相等 B、角平分线就是角的对称轴 C、如果两个角相等，那么这两个角互为对顶角 D、到线段两端点距离相等的点不一定在线段的垂直平分线上

查看试题解析
7. 如果把分式中 $\frac{x + y}{2 x y}$ 的x和y都扩大2倍，那么分式的值（　　）

A、扩大为原来的2倍 B、缩小为原来的 $\frac{1}{2}$ C、不变 D、扩大为原来的4倍

查看试题解析
8. 一个多边形纸片剪去一个内角后，得到一个内角和为2340°的新多边形，则原多边形的边数为（）

A、14或15或16 B、15或16或17 C、15或16 D、16或17

查看试题解析
9. 如图，在 $△ A B C$ 中， $A B = A C ， B C = 10$ ， $S_{△ A B C} = 60$ ， $A D ⊥ B C$ 于点D， $E F$ 垂直平分 $A B$ ，在 $E F$ 上确定一点P，使 $P B + P D$ 最小（　　）

A、10 B、11 C、12 D、13

查看试题解析
10. 如图，已知在正方形 $A B C D$ 中， $A B = B C = C D = A D = 10$ 厘米， $∠ A = ∠ B = ∠ C = ∠ D = 9 0^{°}$ ，点E在边 $A B$ 上，且 $A E = 4$ 厘米，如果点P在线段BC上以2厘米／秒的速度由B点向C点运动，同时，点Q在线段 $C D$ 上由C点向D点运动，设运动时间为t秒，当ΔBPE与ΔCQP全等时，t的值为（　　）

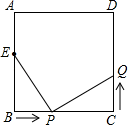A、2 B、2或1.5 C、2.5 D、2.5或2

查看试题解析

二、填空题

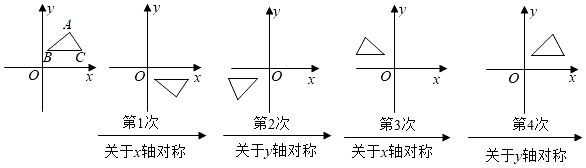
11. 世界上最小的开花结果植物是澳大利亚的出水浮萍，这种植物的果实像一个微小的无花果，质量只有0.000000076克，用科学记数法表示此数是克．

查看试题解析
12. 若 $\frac{\sqrt{x - 1}}{x - 3}$ 在实数范围内有意义，则 $x$ 的取值范围是．

查看试题解析
13. 如果多项式 $4 a^{2} + m a + 25$ 是完全平方式，那么 $m$ 的值是．

查看试题解析
14. 若关于x的分式方程 $\frac{x}{x - 3}$ ﹣2m＝ $\frac{3 m - 1}{x - 3}$ 无解，则m的值为.

查看试题解析
15. 若m为正实数，且m²﹣4m+1＝0，则m²+ $\frac{1}{m^{2}}$ ＝.

查看试题解析
16. 已知等腰三角形两边 $a$ ， $b$ ，满足 $a^{2} + b^{2} - 6 a - 10 b + 34 = 0$ ，则此等腰三角形的周长为．

查看试题解析
17. 在平面直角坐标系中，对 $△ A B C$ 进行循环往复的轴对称变换，若原来点 $A$ 的坐标是 $(\sqrt{3} ， \sqrt{2})$ ，则经过第2021次变换后所得的A点的坐标是．

查看试题解析

三、解答题

18. 计算：

(1)、 $4 {(x + 1)}^{2} - (2 x - 5) (2 x + 5)$

(2)、 $(1 - \frac{1}{a + 1}) \div \frac{a}{a^{2} - 1}$

查看试题解析
19. 因式分解：

(1)、 $5 x^{2} + 10 x + 5$

(2)、 ${(a^{2} + 1)}^{2} - 4 a^{2}$ ．

查看试题解析
20. 解方程：

(1)、 $\frac{x}{x - 2} - 1 = \frac{1}{x^{2} - 4}$

(2)、 $\frac{3 x}{x + 2} + \frac{2}{x - 2} = 3$

查看试题解析
21. 如图， $△ A B C$ 中， $A B = A C$ ，点P在AB上，点Q在线段AC的延长线上， $P B = C Q$ ， PQ与BC相交于点D．点F在BC上，过点P作BC的垂线，垂足为E， $∠ B P E = ∠ F P E$ ．

(1)、求证： $P F = C Q$ ．

(2)、请猜测：线段BE、DE、CD数量关系为．

查看试题解析
22. 因汽车尾气污染引发的雾霾天气备受关注，经市大气污染防治工作领导组研究决定，在市区范围实施机动车单双号限行措施限行期间为方便市民出行，某路公交车每天比原来的运行增加20车次．经调研得知，原来这路公交车平均每天共运送乘客5600人，限行期间这路公交车平均每天共运送乘客7000人，且平均每车次运送乘客与原来的数量基本相同，问限行期间这路公交车每天运行多少车次？

查看试题解析
23.

(1)、【问题背景】
如图1：在四边形 $A B C D$ 中， $A B = A D$ ， $∠ B A D = 120 °$ ， E、F分别是 $B C$ 、 $C D$ 上的点，且 $∠ E A F = 60 °$ ，小王同学探究此问题的方法是：延长 $F D$ 到点G，使 $D G = B E$ ，连接 $A G$ ，再证明 $△ A E F ≅ △ A G F$ ，可得出结论．

(2)、【探索延伸】如图2，若在四边形 $A B C D$ 中， $A B = A D$ ， E、F分别是 $B C$ ， $C D$ 上的点 $\frac{1}{2} ∠ B A D$ ，上述结论是否仍然成立

(3)、【学以致用】
如图3，四边形 $A B C D$ 是边长为5的正方形， $∠ E B F = 45 °$ ，求 $△ D E F$ 的周长．

查看试题解析
24. 综合与探究
如图所示，在平面直角坐标系中，点B、D分别在y轴、x轴上，点 $A (- a ， b)$ ， $C (b ， a)$ ，且a，b满足 $9 a^{2} - 6 a b + b^{2} + {(b - 6)}^{2} = 0$ ， $A B ⊥ y$ 轴于点B， $C D ⊥ x$ 轴于点D．

(1)、直接写出 $a =$ ， $b =$ ；

(2)、如图2，连接AC，BD交于点P，求证：点P为AC中点；

(3)、若 $O C = 2 \sqrt{10}$ ，在x轴上是否存在点F，使 $△ C O F$ 是以 $C O$ 为腰的等腰三角形？若存在，请直接写出F点的坐标；若不存在，请说明理由．

查看试题解析