黑龙江省齐齐哈尔市克东县2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-10-09 类型:期末考试
一、单选题
-
1. 下列所给的四个小篆字中为轴对称图形的是( )A、
 B、
B、 C、
C、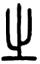 D、
D、 2. 下列各式的计算结果为a7的是( )A、(﹣a)2•(﹣a)5 B、(﹣a)2•(﹣a5) C、(﹣a2)•(﹣a)5 D、(﹣a)•(﹣a)63. 若m为整数,则能使的值也为整数的m有( )A、1个 B、2个 C、3个 D、4个4. 如图,直线a,b相交形成的夹角中,锐角为52°,交点为O,点A在直线a上,直线b上存在点B,使以点O,A,B为顶点的三角形是等腰三角形,这样的点B有( )
2. 下列各式的计算结果为a7的是( )A、(﹣a)2•(﹣a)5 B、(﹣a)2•(﹣a5) C、(﹣a2)•(﹣a)5 D、(﹣a)•(﹣a)63. 若m为整数,则能使的值也为整数的m有( )A、1个 B、2个 C、3个 D、4个4. 如图,直线a,b相交形成的夹角中,锐角为52°,交点为O,点A在直线a上,直线b上存在点B,使以点O,A,B为顶点的三角形是等腰三角形,这样的点B有( ) A、1个 B、2个 C、3个 D、4个5. 已知关于x的分式方程的解是正数,则m的取值范围是( )A、 B、 C、且 D、且6. 如果一个三角形的三边长分别为3,6,a,那么a的值不可能是( )A、4 B、9 C、6 D、87. 下列四个多项式中,能因式分解的是( ).A、a2+1 B、x2+5y C、x2 5y D、a26a+98. 已知:点与点关于x轴对称,则的值为( )A、 B、 C、 D、9. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A、1个 B、2个 C、3个 D、4个5. 已知关于x的分式方程的解是正数,则m的取值范围是( )A、 B、 C、且 D、且6. 如果一个三角形的三边长分别为3,6,a,那么a的值不可能是( )A、4 B、9 C、6 D、87. 下列四个多项式中,能因式分解的是( ).A、a2+1 B、x2+5y C、x2 5y D、a26a+98. 已知:点与点关于x轴对称,则的值为( )A、 B、 C、 D、9. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )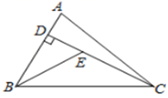 A、5 B、7 C、10 D、310. 如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠CPE的度数是( )
A、5 B、7 C、10 D、310. 如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠CPE的度数是( )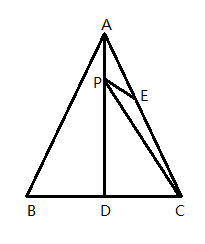 A、30° B、45° C、60° D、90°
A、30° B、45° C、60° D、90°二、填空题
-
11. 如果 x2 -2(m+1)x+m2+5是一个完全平方式,则m= .12. 若分式无意义,则 .13. 已知一个多边形的内角和为540°,则这个多边形是边形.14. 分解因式:2a2﹣8b2=15. 已知:如图, ,只需补充条件 , 就可以根据“ ”得到 .
 16. 等腰三角形一腰上的高与另一腰的夹角为36°,则该等腰三角形的底角的度数为 .17. 如图所示,将多边形分割成三角形、图(1)中可分割出2个三角形;图(2)中可分割出3个三角形;图(3)中可分割出4个三角形;由此你能猜测出,n边形可以分割出个三角形.
16. 等腰三角形一腰上的高与另一腰的夹角为36°,则该等腰三角形的底角的度数为 .17. 如图所示,将多边形分割成三角形、图(1)中可分割出2个三角形;图(2)中可分割出3个三角形;图(3)中可分割出4个三角形;由此你能猜测出,n边形可以分割出个三角形.
三、解答题
-
18. 解方程: +3= .19. 因式分解(1)、(2)、20. 先化简再求值
, 其中 ,
21. 如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E. (1)、若∠B=35°,∠ACB=85°,求∠E的度数;(2)、当P点在线段AD上运动时,猜想∠E与∠B、∠ACB的数量关系,写出结论无需证明.22. 为有效落实双减工作,切实做到减负提质,很多学校决定在课后看护中增加乒乓球项目.体育用品商店得知后,第一次用600元购进乒乓球若干盒,第二次又用600元购进该款乒乓球,但这次每盒的进价是第一次进价的倍,购进数量比第一次少了30盒.(1)、求第一次每盒乒乓球的进价是多少元?(2)、若要求这两次购进的乒乓球按同一价格全部销售完后获利不低于420元,则每盒乒乓球的售价至少是多少元?23. 已知:△ABC中,∠ACB=90°,AC=BC.
(1)、若∠B=35°,∠ACB=85°,求∠E的度数;(2)、当P点在线段AD上运动时,猜想∠E与∠B、∠ACB的数量关系,写出结论无需证明.22. 为有效落实双减工作,切实做到减负提质,很多学校决定在课后看护中增加乒乓球项目.体育用品商店得知后,第一次用600元购进乒乓球若干盒,第二次又用600元购进该款乒乓球,但这次每盒的进价是第一次进价的倍,购进数量比第一次少了30盒.(1)、求第一次每盒乒乓球的进价是多少元?(2)、若要求这两次购进的乒乓球按同一价格全部销售完后获利不低于420元,则每盒乒乓球的售价至少是多少元?23. 已知:△ABC中,∠ACB=90°,AC=BC. (1)、如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;(2)、如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;(3)、如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC=3MC,请直接写出的值.
(1)、如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;(2)、如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;(3)、如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC=3MC,请直接写出的值.