黑龙江省七台河市勃利县2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 在下列长度的四组线段中，能组成三角形的是（）

A、3，7，15 B、1，2，4 C、5，5，10 D、2，3，3

查看试题解析
2. 下列运算正确的是（）

A、 $x^{2} + x^{2} = x^{4}$ B、 $(a - b)^{2} = a^{2} - b^{2}$ C、 $(- a^{2})^{3} = - a^{6}$ D、 $3 a^{2} \cdot 2 a^{3} = 6 a^{6}$

查看试题解析
3. 下列四个图形：
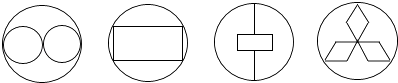
其中是轴对称图形，且对称轴的条数为2的图形的个数是（）

A、4 B、3 C、2 D、1

查看试题解析
4. 使分式 $\frac{x - 3}{2 x - 1}$ 有意义的x的取值范围是(　　)

A、x≥ $\frac{1}{2}$ B、x≤ $\frac{1}{2}$ C、x＞ $\frac{1}{2}$ D、x≠ $\frac{1}{2}$

查看试题解析
5. 如图，AB//DE，AC//DF，AC＝DF，下列条件中，不能判定△ABC≌△DEF的是（）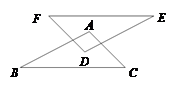

A、AB＝DE B、∠B＝∠E C、EF＝BC D、EF//BC

查看试题解析
6. 若等腰三角形的周长为26cm，一边为11cm，则腰长为（）

A、11cm B、7.5cm C、11cm或7.5cm D、以上都不对

查看试题解析
7. 正多边形的一个内角是 $144 °$ ，则这个正多边形的边数为（　　）

A、10 B、11 C、12 D、13

查看试题解析
8. 若多项式 $x^{2} + a x + b$ 分解因式的结果为 $a (x - 2) (x + 3)$ ，则 $a ， b$ 的值分别为（　　）

A、 $a = 1 ， b = - 6$ B、 $a = 5 ， b = 6$ C、 $a = 1 ， b = 6$ D、 $a = 5 ， b = - 6$

查看试题解析
9. 如图，已知△ABC中，AB=AC，AD=AE，∠BAE=30°，则∠DEC等于（）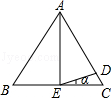

A、7.5° B、10° C、15° D、18°

查看试题解析
10. 分式方程 $\frac{2 - m}{x - 1} = \frac{1}{x}$ 无解，则m的值为（　　）

A、2 B、1 C、1或2 D、0或2

查看试题解析

二、填空题

11. 使分式 $\frac{x^{2} - 1}{x + 1}$ 的值为0，这时x= ．

查看试题解析
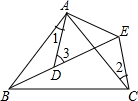
12. 若点 $(m + 2 ， - 3)$ 与点 $(4 ， n + 5)$ 关于x轴对称，则 ${(m n)}^{2} =$ ．

查看试题解析
13. 若4x²－2kx+1是完全平方式，则k= ．

查看试题解析
14. 已知 $a ， b ， c$ 为三角形的三边长，化简 $| a + b - c | + | b - c - a | =$ ．

查看试题解析
15. 如图所示，AB＝AC ， AD＝AE ， ∠BAC＝∠DAE ， ∠1＝25°，∠2＝30°，则∠3＝．

查看试题解析
16. 已知P₁点关于x轴的对称点P₂(3－2a，2a－5)是第三象限内的整点(横、纵坐标都为整数的点，称为整点)，则P₁点的坐标是

查看试题解析
17. 已知：如图，D是 $B C$ 上一点， $A D$ 平分 $∠ B A C$ ， $A B = 3 ， A C = 2$ ，若 $S_{Δ A B D} = a$ ，则 $S_{Δ A D C} =$ ．（用a的代数式表示）

查看试题解析
18. 若 $(m + 58)^{2} = 654483 ， (m + 48) (m + 68) =$ ．

查看试题解析
19. 在Rt△ABC中，∠ACB=90°，BC=2cm，CD⊥AB，在AC上取一点E，使EC=BC，过点E作EF⊥AC交CD的延长线于点F，若EF=5cm，则AE=cm.

查看试题解析
20. 北海到南宁的铁路长210千米，动车运行后的平均速度是原来火车的1.8倍，这样由北海到南宁的行驶时间缩短了1.5小时，设原来火车的平均速度为 $x$ 千米/时，则可列方程为．

查看试题解析

三、解答题

21. 计算

(1)、 $0.25 \times (- 2)^{- 2} \div (16)^{- 1} - (π - 3)^{0}$ ；

(2)、 $(a^{2} b - 2 a b^{2} - b^{3}) \div b - (a + b) (a - b)$ ．

查看试题解析
22. 分解因式

(1)、 $a^{2} (a - b) + b^{2} (b - a)$ ；

(2)、 $3 a x^{2} - 6 a x y + 3 a y^{2}$ ．

查看试题解析
23. 解分式方程

(1)、 $\frac{3 x}{x + 2} + \frac{2}{x - 2} = 3$ ；

(2)、 $\frac{1}{x - 1} - \frac{2}{x + 1} = \frac{4}{x^{2} - 1}$ ．

查看试题解析
24. 先化简再求值： $\frac{a - 1}{a - 2} \div \frac{a 2 - 2 a + 1}{2 a - 4}$ ，其中 $a = - 1$

查看试题解析
25. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（﹣4，5），（﹣1，3）.

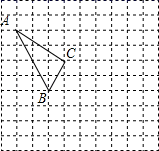
（ 1 ）在如图所示的网格平面内作出平面直角坐标系，标注原点以及x轴、y轴；

（ 2 ）作出△ABC关于y轴对称的△A′B′C′，并写出点B′的坐标；

（ 3 ）点P是x轴上的动点，在图中找出使△A′BP周长最小时的点P，直接写出点P的坐标是：▲.

查看试题解析
26. 如图，D为△ABC的边AB的延长线上一点，过D作DF⊥AC，垂足为F，交BC于E，且BD=BE.求证：△ABC是等腰三角形.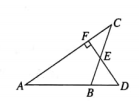

查看试题解析
27. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 90 °$ ，分别过点B，C向过点A的直线作垂线，垂足分别为点E，F．

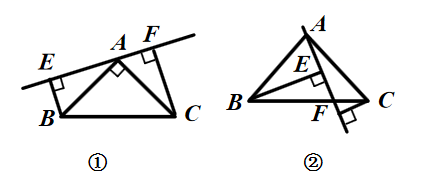(1)、如图①，过点A的直线与斜边BC不相交时，求证：
① $△ A B E ≌ △ C A F$ ；

② $E F = B E + C F$ ．

(2)、如图②，其他条件不变，过点A的直线与斜边BC相交时，若 $B E = 10$ ， $C F = 3$ ，试求EF的长．

查看试题解析
28. 某学校去年在某商场购买甲、乙两种不同足球，购买甲种足球共花费2400元，购买乙种足球共花费1600元，购买甲种足球数量是购买乙种足球数量的2倍．且购买一个乙种足球比购买一个甲种足球多花20元．

(1)、求购买一个甲种足球、一个乙种足球各需多少元；

(2)、今年学校为编排“足球操”，决定再次购买甲、乙两种足球共50个．如果两种足球的单价没有改变，而此次购买甲、乙两种足球的总费用不超过3500元，那么这所学校最少可购买多少个甲种足球？

查看试题解析