黑龙江省宁安市2021-2022学年八年级上学期期末考试数学试题

试卷更新日期：2022-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形是轴对称图形的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 若一个三角形的两边长分别是3和5，则第三边的长可能是（）

A、1 B、2 C、7 D、8

查看试题解析
3. 在 $\frac{2}{x}$ ， $\frac{1}{5}$ ， $\frac{x^{2} + 2}{3}$ ， $\frac{4 x y}{π}$ ， $\frac{5}{x + y}$ ， $2 a + \frac{b}{a}$ 中，分式的个数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
4. 下列计算错误的是（）

A、a³·a^-5=a^-2 B、a⁵÷a^-2=a⁷ C、(-2a²)³= -8a⁵ D、 ${(- 1 + \sqrt{2})}^{0}$ =1

查看试题解析
5. 若代数式 $\frac{\sqrt{3 x}}{x - 2}$ 在实数范围内有意义，则x的取值范围为（）

A、 $x \geq 0 且 x \neq 2$ B、 $x \geq 0$ C、 $x \neq 0$ D、 $x > 0 且 x \neq 2$

查看试题解析
6. 关于x的方程 $\frac{2 a}{x - 1}$ ＝a－1无解，则a的值是（）

A、 $a = 1$ B、 $a = 0$ 或 $a = - 1$ C、 $a = - 1$ D、 $a = 1$ 或 $a = 0$

查看试题解析
7. 等腰 $Δ A B C$ 的底边 $B C = 6 c m$ ，且 $| A C - B C | = 2 c m$ ，则 $A C$ 的长为（）

A、8cm或4cm B、4cm C、6cm D、8cm或6cm

查看试题解析
8. 如图，在△ABC中，点O到三边的距离相等，∠BAC＝60°，则∠BOC＝（）

A、120° B、125° C、130° D、140°

查看试题解析
9. 如图，已知点D、点E分别是等边三角形ABC中BC、AB边的中点，AD＝5，点F是AD边上的动点，则BF＋EF的最小值为（）

A、7.5 B、5 C、4 D、不能确定

查看试题解析
10. 如图所示，H是△ABC的高AD ， BE的交点，且DH=DC ，则下列结论：①BD=AD；②BC=AC；③BH=AC；④CE=CD中正确的有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 已知一粒米的质量约为0.000021kg，将这个数用科学记数法表示为．

查看试题解析
12. 点P关于y轴的对称点P′的坐标是（4，-3），则点P的坐标是．

查看试题解析
13. 已知9 x²+ m x + 16是完全平方式，则m = ．

查看试题解析
14. 如图所示，AB=AE，∠EAB=∠FAC，请添加一个条件，使△ABC≌△AEF，这个添加的条件可以是（只需写一个，不添加辅助线）．

查看试题解析
15. 如图所示，AB＝AC ， AD＝AE ， ∠BAC＝∠DAE ， ∠1＝25°，∠2＝30°，则∠3＝．

查看试题解析
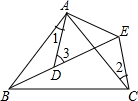16. 如图，在△ABC中，AB，AC的垂直平分线交BC于点E，G，若∠B+∠C=70°，则∠EAG=.

查看试题解析
17. 一列数： $\frac{1}{2} ， \frac{2}{5} ， \frac{3}{10} ， \frac{4}{17} ， \frac{5}{26}$ ， …，它们按一定的规律排列，则第n个数(n为正整数)为．

查看试题解析
18. 一个等腰三角形的一个外角等于130°，则这个等腰三角形的顶角度数是度．

查看试题解析
19. 已知OC平分∠AOB，点P为OC上一点，PD⊥OA于D，且PD=3cm，过点P作PE∥OA交OB于E，∠AOB=30°，求PE的长度cm．

查看试题解析
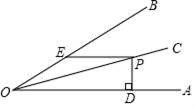20. 如图所示，点D在∠BAC的角平线上，DE⊥AB于点E，DF⊥AC于点F，连接EF，BC⊥AD于点D，则下列结论中①DE＝DF；②AE＝AF；③∠ABD＝∠ACD；④∠EDB＝∠FDC，其中正确的序号是．

查看试题解析

三、解答题

21. 计算： $(2 a + b) (2 a - b) - b (2 a - b) - 4 a^{2} b \div b$

查看试题解析
22. 先化简，再求值： $\frac{x - 3}{x^{2} - 4} \cdot \frac{x^{2} + 4 x + 4}{x - 3} - (\frac{2}{x - 2} + 1)$ ，其中 $x = \frac{2}{3}$ .

查看试题解析
23. 如图，在直角坐标系中，A（﹣1，5），B（﹣3，0），C（﹣4，3）.

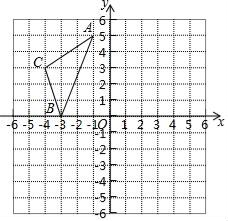(1)、在图中作出△ABC关于y轴对称的图形△A₁B₁C₁；

(2)、写出点C₁的坐标；

(3)、求△ABC的面积.

查看试题解析
24. $Δ A B C$ 中， $∠ B = 30 ° ，$ $A D$ 为边BC上的高，且 $∠ D A C = 20 °$ ，请画出符合条件的图形，并直接写出 $∠ B A C$ 度数.

查看试题解析
25. 如图，DE⊥AB于E，DF⊥AC于F，若BD = CD，BE = CF．
求证：

(1)、AD平分∠BAC；

(2)、AC=AB+2BE.

查看试题解析
26. 在 $Δ A B C$ 中， $∠ A B C = 90 ° ， A B = B C$ ，点O是AC的中点，过A、B两点向经过点O的直线作垂线，垂足分别为E、F．

(1)、如图①，求证：EF=AE+BF；

(2)、如图②、如图③，线段EF，AE，BF又有怎样的数量关系？请你写出猜想，不需证明；

(3)、若 $A E = \sqrt{3} B F = 2 \sqrt{3}$ ，则 $E F$ = ．

查看试题解析
27. 2021年是中国共产党百年华诞，某电脑公司为了庆祝党的生日，开展回馈顾客活动，在七月份把甲种型号电脑的售价每台降低1000元，如果在六月份和七月份卖出相同数量的电脑，六月份销售额为10万元，七月份销售额只有8万元．
请解答下列问题：

(1)、七月份甲种型号电脑每台售价多少元？

(2)、为了满足不同顾客需要，电脑公司决定再经销乙种型号电脑，已知甲种电脑每台进价为3500元，乙种型号电脑每台进价为3000元，公司预计用不少于4.8万元的资金购进这两种电脑共15台，且甲种型号电脑至多8台，有哪几种进货方案？

(3)、在（2）的条件下，如果乙种型号电脑每台售价为3800元，哪种方案对公司更有利？公司的利润是多少？(请直接写出结果．)

查看试题解析
28. 如图，在平面直角坐标系中 $A (a ， 0) ， B (0 ， b)$ ，满足 $a^{2} - 4 a + 4 + | b - 4 | = 0$

(1)、求 $A ， B$ 两点的坐标；

(2)、 $∠ O B A$ 的平分线 $B C$ 与 $∠ O A B$ 的外角平分线AM交于点C，求 $∠ C$ 的度数；

(3)、在平面内是否存在点P，使 $Δ A B P$ 为等腰直角三角形？若存在，请写出点P的个数，并直接写出其中两个点的坐标；若不存在，请说明理由.

查看试题解析