黑龙江省牡丹江市林口县2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，是轴对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 一个三角形的三边长分别为x、3、4，那么x的取值范围是（　　）

A、1＜x＜4 B、1＜x＜7 C、1≤x＜7 D、x＞1

查看试题解析
3. 下列计算中，正确的是（　　）

A、 $(- 3)^{- 2} = - \frac{1}{9}$ B、 $x^{4} \cdot x^{2} = x^{8}$ C、 $(a^{2})^{3} \cdot a^{3} = a^{9}$ D、 $(a - 2)^{0} = 1$

查看试题解析
4. 如图，已知∠1=∠2，若用“SAS”证明△ACB≌△BDA，还需加上条件（）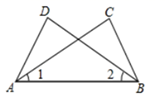

A、AD ＝BC B、BD＝AC C、∠D＝∠C D、OA＝OB

查看试题解析
5. 一个正多边形的每一个内角都等于135°，那么从这个多边形的一个顶点可以引对角线的条数是（）

A、4条 B、5条 C、6条 D、8条

查看试题解析
6. 若x²+（k﹣1）x+4是一个完全平方式，则常数k的值为（　　）

A、5 B、5或3 C、﹣3 D、5或-3

查看试题解析
7. 如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，S_△_ABC＝24，DE＝4，AB＝7，则AC长是（）

A、3 B、4 C、6 D、5

查看试题解析
8. 如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE中点，且△ABC的面积等于4cm² ，则阴影部分图形面积等于（）.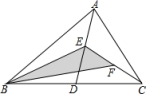

A、1cm² B、2cm² C、0.5cm² D、1.5cm²

查看试题解析
9. 已知甲做360个零件与乙做480个零件所用的时间相同，两人每天共做140个零件，设甲每天做x个零件，根据题意，可列方程为（）

A、 $\frac{360}{x} = \frac{480}{140 - x}$ B、 $\frac{360}{140 - x} = \frac{480}{x}$ C、 $\frac{360}{x} + \frac{480}{x} = 140$ D、 $\frac{360}{x} - 140 = \frac{480}{x}$

查看试题解析
10. 若a，b为等腰△ABC的两边，且满足|a﹣4|+ $\sqrt{b - 2}$ ＝0，则△ABC的周长为（　　）

A、8 B、10 C、8或12 D、8或10

查看试题解析
11.
如图，四边形ABCD中，点M，N分别在AB，BC上，将△BMN沿MN翻折，得△FMN，若MF∥AD，FN∥DC，则∠B=（　　）

A、60° B、70° C、80° D、90°

查看试题解析
12. 如图，已知△ABC中高AD恰好平分边BC，∠B=30°，点P是BA延长线上一点，点O是线段AD上一点且OP=OC，下面的结论：①∠APO+∠DCO=30°；②△OPC是等边三角形；③AC=AO+AP；④S_△ABC=S_四_边_形AOCP．其中正确的为（）

A、①②③④ B、①②③ C、②③ D、②③④

查看试题解析

二、填空题

13. 小时候我们用肥皂水吹泡泡，其泡沫的厚度约0.000326毫米，0.000326毫米用科学记数法表示正确的是毫米.

查看试题解析
14. 若分式 $\frac{x^{2} - 4}{x + 2}$ 的值为0，则x= ．

查看试题解析
15. 已知关于 x 的分式方程 $\frac{m}{x - 1} + \frac{3}{1 - x} = 1$ 的解是非负数，
则 m 的取值范围是.

查看试题解析
16. 在△ABC中，AB=AC，AB的垂直平分线交AB于点D，交直线AC于点E，∠AEB=80°，那么∠BAC等于．

查看试题解析
17. 分解因式m³+2m²+m＝．

查看试题解析
18. 下列命题：①关于某条直线成轴对称的两个图形是全等图形；②有一个外角为60°的等腰三角形是等边三角形；③关于某直线对称的两条线段平行；④正五边形有五条对称轴；⑤在直角三角形中，30°角所对的边等于斜边的一半．其中正确的有．（填序号）

查看试题解析
19. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 20 °$ ， $P Q$ 垂直平分 $A B$ ，垂足为Q，交 $B C$ 于点P．按以下步骤作图：①以点A为圆心，以适当的长为半径作弧，分别交边 $A C ， A B$ 于点D，E；②分别以点D，E为圆心，以大于 $\frac{1}{2} D E$ 的长为半径作弧，两弧相交于点F；⑤作射线 $A F$ ．若 $A F$ 与 $P Q$ 的夹角为 $α$ ，则 $α =$ °．

查看试题解析
20. 如图，将等边△ABC折叠，使得点B恰好落在AC边上的点D处，折痕为EF，O为折痕EF上一动点，若AD=1，AC=3，△OCD周长的最小值是．

查看试题解析

三、解答题

21.

(1)、计算：a（2﹣a）+（a+b）（a﹣b）．

(2)、解方程： $\frac{3}{2 x + 3} = \frac{1}{x + 1}$

(3)、先化简，再求值： $\frac{x^{2} + 2 x}{x - 1} \cdot \frac{1}{x} - \frac{x}{x - 1}$ ，其中x＝2．

查看试题解析
22. △ABC在平面直角坐标系中的位置如图所示，A、
B、C三点在格点(小正方形的顶点)上.

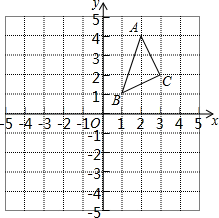(1)、作出△ABC关于x轴对称的△A₁B₁C₁ ，写出点A₁、B₁、C₁的坐标；

(2)、求△ABC的面积.

查看试题解析
23. 在△ABC中，∠B＝25°，∠A＝100°，点P在△ABC的三边上运动，当△PAC成为等腰三角形时，其顶角的度数是多少度呢？请画出图形，在相应图形下方直接写出答案．

查看试题解析
24. 如图，在△ABC中，AB ＝AC ， AD⊥BC于点D ， AM是△ABC的外角∠CAE的平分线．

(1)、求证：AM∥BC；

(2)、若DN平分∠ADC交AM于点N，判断△ADN的形状并说明理由．

查看试题解析
25. 已知△ABC和△ADE都是等腰直角三角形，点D是直线BC上的一动点（点D不与B、C重合），连接CE，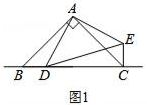

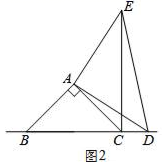
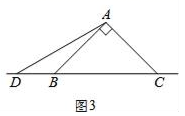(1)、在图1中，当点D在边BC上时，求证：BC=CE+CD；

(2)、在图2中，当点D在边BC的延长线上时，结论BC=CE+CD是否还成立？若不成立，请猜想BC、CE、CD之间存在的数量关系，并说明理由；

(3)、在图3中，当点D在边BC的反向延长线上时，补全图形，不需写证明过程，直接写出BC、CE、CD之间存在的数量关系．

查看试题解析
26. 为抗击新型冠状病毒，某药店计划购进一批甲、乙两种型号的口罩，已知一袋甲种口罩的进价与一袋乙种口罩的进价和为40元，用90元购进甲种口罩的袋数与用150元购进乙种口罩的袋数相同．

(1)、求每袋甲种、乙种口罩的进价分别是多少元?

(2)、该药店计划购进甲、乙两种口罩共480袋，其中甲种口罩的袋数少于乙种口罩袋数的 $\frac{17}{23}$ ，药店计划此次进货的总资金不超过10000元，求药店共有几种进货方案?

查看试题解析