黑龙江省佳木斯市抚远市2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-10-09 类型:期末考试
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 若把分式中的x和y都扩大3倍,则分式的值( )A、扩大3倍 B、缩小6倍 C、缩小3倍 D、不变4. 已知等腰三角形的一个底角为70°,则其顶角为( )A、50° B、60° C、30° D、40°5. 一个等腰三角形的两边长分别为3,6,则这个等腰三角形的周长是( )A、 B、或 C、 D、无法确定6. 下列式子从左到右变形是因式分解的是( )A、 B、 C、 D、7. 如果一个多边形的每个内角的度数都是108°,那么这个多边形的边数是( )A、3 B、4 C、5 D、68. 关于x的分式方程的解为正数,则m的取值范围是( )A、 B、 C、且 D、且9. 有两块面积相同的试验田,分别收获蔬菜900kg和1500kg,已知第一块试验田每亩收获蔬菜比第二块少300kg,求第一块试验田每亩收获蔬菜多少千克.设第一块试验田每亩收获蔬菜xkg,根据题意,可得方程( )A、 B、 C、 D、10. 如图,在锐角三角形ABC中, , BE,CD为的角平分线.BE,CD交于点F,FG平分 , 有下列四个结论:①;②;③≌;④ . 其中结论正确的序号有( ).
3. 若把分式中的x和y都扩大3倍,则分式的值( )A、扩大3倍 B、缩小6倍 C、缩小3倍 D、不变4. 已知等腰三角形的一个底角为70°,则其顶角为( )A、50° B、60° C、30° D、40°5. 一个等腰三角形的两边长分别为3,6,则这个等腰三角形的周长是( )A、 B、或 C、 D、无法确定6. 下列式子从左到右变形是因式分解的是( )A、 B、 C、 D、7. 如果一个多边形的每个内角的度数都是108°,那么这个多边形的边数是( )A、3 B、4 C、5 D、68. 关于x的分式方程的解为正数,则m的取值范围是( )A、 B、 C、且 D、且9. 有两块面积相同的试验田,分别收获蔬菜900kg和1500kg,已知第一块试验田每亩收获蔬菜比第二块少300kg,求第一块试验田每亩收获蔬菜多少千克.设第一块试验田每亩收获蔬菜xkg,根据题意,可得方程( )A、 B、 C、 D、10. 如图,在锐角三角形ABC中, , BE,CD为的角平分线.BE,CD交于点F,FG平分 , 有下列四个结论:①;②;③≌;④ . 其中结论正确的序号有( ).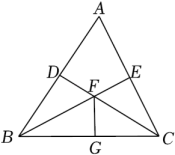 A、①②③ B、①②④ C、②③④ D、①③④
A、①②③ B、①②④ C、②③④ D、①③④二、填空题
-
11. 世纪纳米技术将被广泛应用.纳米是长度的度量单位,1纳米=0.000000001米,则5纳米用科学记数法表示为米.12. 如图,点在上,点E在上, , 添加一个条件 , 使(填一个即可).
 13. 若分式 有意义,则 的取值范围是.14.
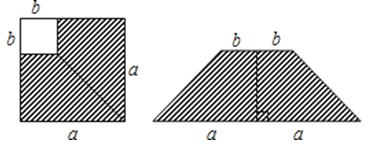
13. 若分式 有意义,则 的取值范围是.14.如图,在边长为a的正方形中剪去一个边长为b的小正方形(a>b),把剩下的部分拼成一个梯形,分别计算这两个图形阴影部分的面积,验证了公式 .
 15. 若x2+kx+25是一个完全平方式,则k的值是.16. 化简 的结果是17. 如图所示,在正方形ABCD中,以AB为边向正方形外作等边三角形ABE , 连接CE、BD交于点G , 连接AG , 那么∠AGD的底数是度.
15. 若x2+kx+25是一个完全平方式,则k的值是.16. 化简 的结果是17. 如图所示,在正方形ABCD中,以AB为边向正方形外作等边三角形ABE , 连接CE、BD交于点G , 连接AG , 那么∠AGD的底数是度.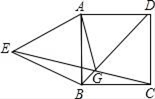 18. 如图,在 中, , , , , 是 的平分线.若 , 分别是 和 上的动点,则 的最小值是.
18. 如图,在 中, , , , , 是 的平分线.若 , 分别是 和 上的动点,则 的最小值是.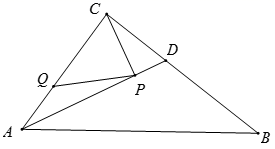 19. 如图.已知中,厘米, , 厘米,D为的中点.如果点P在线段上以2厘米/秒的速度由点B向点C运动,同时,点Q在线段上由点C向点A运动.若点Q的运动速度为a厘米/秒,则当与全等时,a的值为 .
19. 如图.已知中,厘米, , 厘米,D为的中点.如果点P在线段上以2厘米/秒的速度由点B向点C运动,同时,点Q在线段上由点C向点A运动.若点Q的运动速度为a厘米/秒,则当与全等时,a的值为 .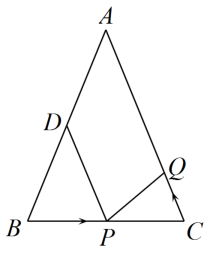 20. 观察下列图形,第一个图形中有一个三角形;第二个图形中有5个三角形;第三个图形中有9个三角形;….则第2021个图形中有个三角形.
20. 观察下列图形,第一个图形中有一个三角形;第二个图形中有5个三角形;第三个图形中有9个三角形;….则第2021个图形中有个三角形.
三、解答题
-
21. 计算(1)、因式分解:;(2)、解方程: .22. 先化简 , 再从0,-2,-1,1中选择一个合适的数代入并求值.23. 如图,方格纸中每个小正方形的边长都是1个单位长度.在平面直角坐标系中的位置如图所示.
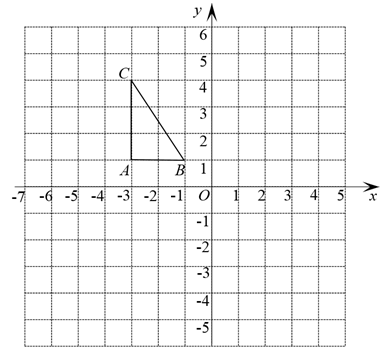 (1)、将向右平移4个单位长度后,得到 , 请画出;(2)、作关于x轴对称的;(3)、连接 , , , 得到 , 求出的面积.24. 如图,已知 . 求证: .
(1)、将向右平移4个单位长度后,得到 , 请画出;(2)、作关于x轴对称的;(3)、连接 , , , 得到 , 求出的面积.24. 如图,已知 . 求证: .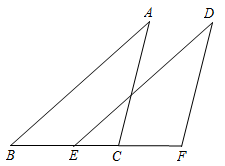 25. 如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.
25. 如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.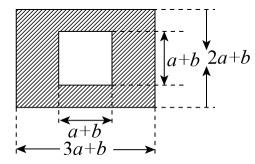 (1)、绿化的面积是多少平方米?(2)、并求出当a=3,b=2时的绿化面积.26. 在中, , , 点D在直线上,以为边作正方形 . 连接 .
(1)、绿化的面积是多少平方米?(2)、并求出当a=3,b=2时的绿化面积.26. 在中, , , 点D在直线上,以为边作正方形 . 连接 .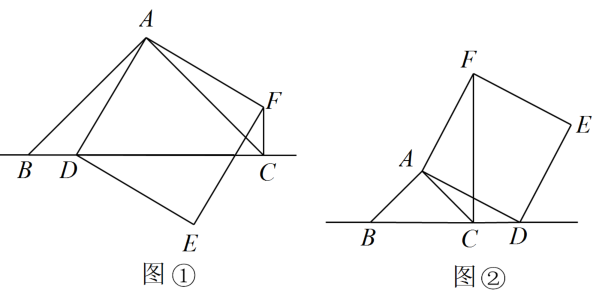
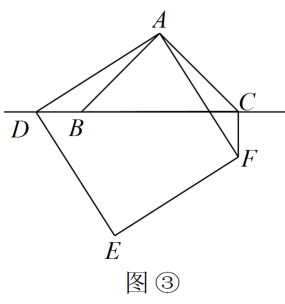 (1)、当点D在线段上时,如图①.易证:(不需证明):(2)、当点D在的延长线上时,如图②,写出 , 与之间的关系,并给出证明;(3)、当点D在的延长线上时.如图③.直接写出 , 与之间的关系.27. 某中学组织学生去福利院慰问,在准备礼品时发现,购买1个甲礼品比购买1个乙礼品多花40元,并且花费600元购买甲礼品和花费360元购买乙礼品的数量相等.
(1)、当点D在线段上时,如图①.易证:(不需证明):(2)、当点D在的延长线上时,如图②,写出 , 与之间的关系,并给出证明;(3)、当点D在的延长线上时.如图③.直接写出 , 与之间的关系.27. 某中学组织学生去福利院慰问,在准备礼品时发现,购买1个甲礼品比购买1个乙礼品多花40元,并且花费600元购买甲礼品和花费360元购买乙礼品的数量相等.
(1)、求甲、乙两种礼品的单价各为多少元?(2)、学校准备购买甲、乙两种礼品共30个送给福利院的老人,要求购买礼品的总费用不超过2000元,那么最多可购买多少个甲礼品?28. 如图,在平面直角坐标系中,在x轴上,点B在y轴上,且 . 平分 . 交于点E,交y轴于点D,F是x轴上一点.且 .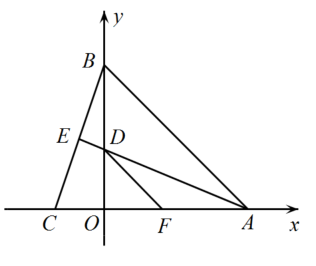 (1)、求点A与点C的坐标:(2)、求证::(3)、P为x轴上一动点, , 是以为腰的等腰角形,直接写出点P的坐标.
(1)、求点A与点C的坐标:(2)、求证::(3)、P为x轴上一动点, , 是以为腰的等腰角形,直接写出点P的坐标.