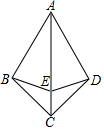黑龙江省鸡西市密山市2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-10-09 类型:期末考试
一、单选题
-
1. 下列图形中,不是轴对称图形的是 ( )
 A、①⑤ B、②⑤ C、④⑤ D、①③2. 下列各组线段能组成一个三角形的是( ).A、3cm,3cm,6cm B、2cm,3cm,6cm C、5cm,8cm,12cm D、4cm,7cm,11cm3. 已知三角形两个内角的差等于第三个内角,则它是( )A、锐角三角形 B、钝角三角形 C、直角三角形 D、等边三角形4. 下列说法错误的是( )A、关于某条直线对称的两个三角形一定全等 B、轴对称图形至少有一条对称轴 C、两个全等三角形一定能关于基本条直线对称 D、角是关于它的平分线所在直线对称的图形5. 如图,AD是△ABC的中线,CE是△ACD的中线,DF是△CDE的中线,若S△DEF=4,则S△ABC等于( )
A、①⑤ B、②⑤ C、④⑤ D、①③2. 下列各组线段能组成一个三角形的是( ).A、3cm,3cm,6cm B、2cm,3cm,6cm C、5cm,8cm,12cm D、4cm,7cm,11cm3. 已知三角形两个内角的差等于第三个内角,则它是( )A、锐角三角形 B、钝角三角形 C、直角三角形 D、等边三角形4. 下列说法错误的是( )A、关于某条直线对称的两个三角形一定全等 B、轴对称图形至少有一条对称轴 C、两个全等三角形一定能关于基本条直线对称 D、角是关于它的平分线所在直线对称的图形5. 如图,AD是△ABC的中线,CE是△ACD的中线,DF是△CDE的中线,若S△DEF=4,则S△ABC等于( ) A、16 B、24 C、32 D、306. 下列计算正确的是( )A、3a2﹣4a2=a2 B、a2•a3=a6 C、a10÷a5=a2 D、(a2)3=a67. 下列各式中,与(1-a)2相等的是( )A、a2-1 B、a2-2a+1 C、a2-2a-1 D、a2+18. 如图,在等边△ABC中,BD平分∠ABC交AC于点D,过点D作DE⊥BC于点E,且CE=3,则AB的长为( )
A、16 B、24 C、32 D、306. 下列计算正确的是( )A、3a2﹣4a2=a2 B、a2•a3=a6 C、a10÷a5=a2 D、(a2)3=a67. 下列各式中,与(1-a)2相等的是( )A、a2-1 B、a2-2a+1 C、a2-2a-1 D、a2+18. 如图,在等边△ABC中,BD平分∠ABC交AC于点D,过点D作DE⊥BC于点E,且CE=3,则AB的长为( ) A、16 B、12 C、9 D、109. 如图,AD是△ABC 的角平分线,DF⊥AB,垂足为F,且DE=DG,则∠AED+∠AGD和是( )
A、16 B、12 C、9 D、109. 如图,AD是△ABC 的角平分线,DF⊥AB,垂足为F,且DE=DG,则∠AED+∠AGD和是( ) A、180° B、200° C、210° D、240°10. 如图,OP平分∠MON,PE⊥OM于点E,PF⊥ON于点F,OA=OB,则图中有( )对全等三角形.
A、180° B、200° C、210° D、240°10. 如图,OP平分∠MON,PE⊥OM于点E,PF⊥ON于点F,OA=OB,则图中有( )对全等三角形. A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
11. 当x时,分式无意义.12. 如果一个多边形的内角和为1260°,那么从这个多边形的一个顶点可以连条对角线.13. 如图所示,三角形的两边长分别是4cm和6cm,则第三边长x的范围是
 14. 点 关于直线 对称的点的坐标是15. 等腰三角形的一个内角是40°,则其他两角的度数分别是16. 若 ,则 = .17. 已知x2-2x-3=0,则2x2-4x=18. 如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.当∠A=40°时,则∠DEF的度数为 .
14. 点 关于直线 对称的点的坐标是15. 等腰三角形的一个内角是40°,则其他两角的度数分别是16. 若 ,则 = .17. 已知x2-2x-3=0,则2x2-4x=18. 如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.当∠A=40°时,则∠DEF的度数为 .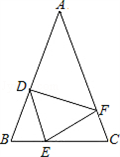 19. 如图,在△ABC 中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.若AB=8cm,△MBC的周长是14cm.若点P为直线 MN上一点,则△PBC周长的最小值是
19. 如图,在△ABC 中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.若AB=8cm,△MBC的周长是14cm.若点P为直线 MN上一点,则△PBC周长的最小值是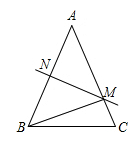 20. 如图,△ABC,△DCE都是等边三角形,则①AE=BD,②△ABD≌△BCD,③∠BAE=∠ACE,④△BCD≌△ACE,⑤∠BDC=∠AEC,以上正确的序号是
20. 如图,△ABC,△DCE都是等边三角形,则①AE=BD,②△ABD≌△BCD,③∠BAE=∠ACE,④△BCD≌△ACE,⑤∠BDC=∠AEC,以上正确的序号是
三、解答题
-
21. 计算题:(1)、(2)、(3)、(4)、(5)、22.(1)、先化简,再求值: ,其中x=(2)、已知 , 求的值.23. 如图,AB=AC,∠BAD=∠CAD,证明:△ABD≌△ACD
 24. 甲、乙两种机器人都被用来搬运化工原料,甲型机器人比乙型机器人每小时多搬运30千克,甲型机器人搬运900千克所用时间与乙型机器人搬运600千克所用时间相等,两种机器人每小时分别搬运多少化工原料?25. 如图:点B,E,C,F在一条直线上,FB=CE,AB//ED,AC//DF.求证: AB=DE,AC=DF.
24. 甲、乙两种机器人都被用来搬运化工原料,甲型机器人比乙型机器人每小时多搬运30千克,甲型机器人搬运900千克所用时间与乙型机器人搬运600千克所用时间相等,两种机器人每小时分别搬运多少化工原料?25. 如图:点B,E,C,F在一条直线上,FB=CE,AB//ED,AC//DF.求证: AB=DE,AC=DF.