黑龙江省黑河市逊克县2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-10-09 类型:期末考试
一、单选题
-
1. 如图所示几何图形中,一定是轴对称图形的有( )个
 A、2 B、3 C、4 D、52. 等腰三角形的两边分别为3cm,4cm,则它的周长是( )A、10cm B、11cm C、16cm或9cm D、10cm或11cm3. 若一个凸多边形的内角和为720°,则这个多边形的边数为A、4 B、5 C、6 D、74. 点N(a,﹣b)关于x轴的对称点的坐标是( )A、(a,b) B、(﹣a,﹣b) C、(-a,b) D、(﹣b,a)5. 下列运算正确的是( )A、 B、 C、 D、6. 有下列方程:①2x+=10;②x-;③;④ . 属于分式方程的有( )A、①② B、②③ C、③④ D、②④7. 下列条件,不能判定的是( )A、 , , B、 , , C、 , , D、 , ,8. 下列说法错误的是( )A、如果两个图形全等,那么它们的形状和大小一定相同; B、图形全等,只与形状,大小有关,而与它们的位置无关; C、全等图形的面积相等,面积相等的两个图形是全等图形; D、全等三角形的对应边相等,对应角相等.9. 要使分式有意义,则x应满足条件( )A、x≠1 B、x≠﹣2 C、x>1 D、x>﹣210. 如图所示, , , , 结论:①;②;③;④ , 其中正确的是有( )
A、2 B、3 C、4 D、52. 等腰三角形的两边分别为3cm,4cm,则它的周长是( )A、10cm B、11cm C、16cm或9cm D、10cm或11cm3. 若一个凸多边形的内角和为720°,则这个多边形的边数为A、4 B、5 C、6 D、74. 点N(a,﹣b)关于x轴的对称点的坐标是( )A、(a,b) B、(﹣a,﹣b) C、(-a,b) D、(﹣b,a)5. 下列运算正确的是( )A、 B、 C、 D、6. 有下列方程:①2x+=10;②x-;③;④ . 属于分式方程的有( )A、①② B、②③ C、③④ D、②④7. 下列条件,不能判定的是( )A、 , , B、 , , C、 , , D、 , ,8. 下列说法错误的是( )A、如果两个图形全等,那么它们的形状和大小一定相同; B、图形全等,只与形状,大小有关,而与它们的位置无关; C、全等图形的面积相等,面积相等的两个图形是全等图形; D、全等三角形的对应边相等,对应角相等.9. 要使分式有意义,则x应满足条件( )A、x≠1 B、x≠﹣2 C、x>1 D、x>﹣210. 如图所示, , , , 结论:①;②;③;④ , 其中正确的是有( )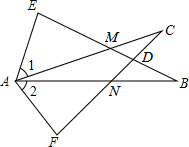 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如果一个正多边形的一个外角是60°,那么这个正多边形的边数是.12. 已知实数x,y满足xy=3,x+y=7,则代数式x2y+xy2的值是13. 在等腰三角形中,已知一个角为40°,那么另两个角的度数是.14. 现要用两种不同的正多边形地砖铺地板,若已选用正方形,则还可以选用形与它搭配铺成无空隙且不重叠的地面(只需要写出一种即可)15. 如图,已知BD=AC , 那么添加一个条件后,能得到△ABC≌△BAD(只填一个即可).
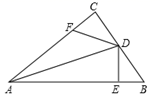
 16. 若代数式 是一个完全平方式,则k是 .17. 如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=7cm,CE=5cm,则DE=cm.
16. 若代数式 是一个完全平方式,则k是 .17. 如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=7cm,CE=5cm,则DE=cm. 18. 如图,中,DE是AC的垂直平分线, , 的周长为16cm,则的周长为 .
18. 如图,中,DE是AC的垂直平分线, , 的周长为16cm,则的周长为 . 19. 分式 当x 时,分式的值为零.20. 已知关于x的方程=1的解是正数,则a的取值范围是 .
19. 分式 当x 时,分式的值为零.20. 已知关于x的方程=1的解是正数,则a的取值范围是 .三、解答题
-
21.(1)、计算:(a+b)2-(a-b)2;(2)、解方程:22. 因式分解:m3-2m2n+mn223. 在如图的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线交点的三角形)ABC的顶点A,C的坐标分别为(-3,4),(0,2).
 (1)、请在网格平面内作出平面直角坐标系;(2)、请作出△ABC关于y轴对称的;并直接写出点的坐标.
(1)、请在网格平面内作出平面直角坐标系;(2)、请作出△ABC关于y轴对称的;并直接写出点的坐标.