黑龙江省哈尔滨市五常市2021-2022学年八年级上学期期末数学试题2

试卷更新日期：2022-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 在下列长度的各组线段中，能组成三角形的是（）

A、2，4，7 B、1，4，9 C、3，4，5 D、5，6，12

查看试题解析
2. 下列运算错误的是（）

A、x²•x³=x⁵ B、（x²）³=x⁶ C、x³+x³=2x⁶ D、（﹣2x）³=﹣8x³

查看试题解析
3. 能使分式 $\frac{| x | - 1}{x^{2} - 2 x + 1}$ 的值为零的所有x的值是（）

A、x=1 B、x=﹣1 C、x=1或x=﹣1 D、x=2或x=1

查看试题解析
4. 已知一个等腰三角形的两边长分别是4，5，则它的周长是（）

A、13 B、14 C、13或14 D、9或12

查看试题解析
5. 若分式 $\frac{x^{2}}{x^{2} + x}$ 化简为 $\frac{x}{x + 1}$ ，则 $x$ 应满足的条件是（）

A、 $x \neq 1$ 或 $x \neq 0$ B、 $x \neq - 1$ 且 $x \neq 0$ C、 $x \neq - 1$ D、 $x \neq 0$

查看试题解析
6. 如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（）

A、锐角三角形 B、钝角三角形 C、直角三角形 D、不能确定

查看试题解析
7. 如果把分式 $\frac{x y}{x + y}$ 中的x和y都扩大为原来的2倍，那么分式的值（）

A、扩大为原来的4倍 B、扩大为原来的2倍 C、不变 D、缩小为原来的的 $\frac{1}{2}$

查看试题解析
8. 若 $y - x = - 1$ ， $x y = 2$ ，则代数式 $- \frac{1}{2} x^{3} y + x^{2} y^{2} - \frac{1}{2} x y^{3}$ 的值是（）

A、2 B、－2 C、1 D、－1

查看试题解析
9. 如图，由4个小正方形组成的田字格中，△ABC的顶点都是小正方形的顶点，在田字格上画与△ABC成轴对称的三角形，且顶点都是小正方形的顶点，则这样的三角形(不包含△ABC本身)共有（）

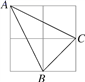A、1个 B、3个 C、2个 D、4个

查看试题解析
10. 如图，∠MON内有一点P，P点关于OM的轴对称点是G，P点关于ON的轴对称点是H，GH分别交OM、ON于A、B点，若∠MON=35°，则∠GOH=（）

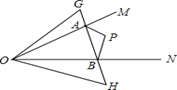A、60° B、70° C、80° D、90°

查看试题解析

二、填空题

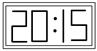
11. 点M（3，﹣4）关于x轴的对称点的坐标是．

查看试题解析
12. 在平面镜里看到背后墙上的电子钟示数如图所示，这时的实际时间应该是.

查看试题解析
13. 三角形的三边长分别为5，1+2x，8，则x的取值范围是.

查看试题解析
14. 分解因式： $3 x^{3} - 12 x^{2} y + 12 x y^{2} =$ ．

查看试题解析
15. 用科学记数法表示： $0.001685 \approx$ ．（精确到万分位）

查看试题解析
16. 如图，△ABC中，AC的垂直平分线交AC于E，交BC于D，△ABD周长为13cm，AE＝4.5cm，则△ABC周长为．

查看试题解析
17. 如图，BD是∠ABC的平分线，DE⊥AB于点E，DF⊥BC于点F，AB＝12，BC＝15，△ABC的面积是36，则DE的长是．

查看试题解析
18. 若关于x的分式方程 $\frac{x}{x - 3}$ ﹣2m＝ $\frac{3 m - 1}{x - 3}$ 无解，则m的值为.

查看试题解析
19. 一个凸 $n$ 边形的边数与对角线条数的和小于20，且能被5整除，则 $n =$ ．

查看试题解析
20. 如图，点E是CD上的一点，Rt△ACD≌Rt△EBC，则下结论：①AC＝BC，②AD∥BE，③∠ACB＝90°，④AD+DE＝BE，
成立的有个．

查看试题解析

三、解答题

21. 作图题：（不要求写作法）如图，△ABC在平面直角坐标系中，其中，点A、B、C的坐标分别为A（﹣2，1），B（﹣4，5），C（﹣5，2）．

(1)、作△ABC关于直线l：x＝﹣1对称的△A₁B₁C₁ ，其中，点A、B、C的对应点分别为A₁、B₁、C₁；

(2)、写出点A₁、B₁、C₁的坐标．

查看试题解析
22. 已知 $x$ ， $y$ 满足等式 $| x - 1 | + {(y - 2)}^{2} = 0$ ，求 $\frac{x^{2} - y^{2}}{x^{2} + 2 x y + y^{2}}$ 的值．

查看试题解析
23. 先化简，再求值： $\frac{a - 3}{a - 2}$ ÷( $\frac{5}{2 - a}$ +a+2)，其中a满足等式|a+1|＝0．

查看试题解析
24. 如图，在 $△ A B C$ 中，AB＝AC，点D是BC上一点，点E是AC上一点，且DE⊥AD.若∠BAD＝55°，∠B＝50°，求∠DEC的度数.

查看试题解析
25.

(1)、画图探究：如图①，若点 $A$ ， $B$ 在直线 $m$ 的同侧，在直线 $m$ 上求作一点 $P$ ，使 $A P + B P$ 的值最小，保留作图痕迹，不写作法；

(2)、实践运用：如图②，等边 $△ A B C$ 的边 $B C$ 上的高为6， $A D$ 是边 $B C$ 上的中线， $M$ 是 $A D$ 上的动点， $E$ 是 $A C$ 的中点，求 $E M + C M$ 的最小值．

查看试题解析
26. 某工厂计划在规定时间内生产24000个零件．若每天比原计划多生产30个零件，则在规定时间内可以多生产300个零件．

(1)、求原计划每天生产的零件个数和规定的天数

(2)、为了提前完成生产任务，工厂在安排原有工人按原计划正常生产的同时，引进5组机器人生产流水线共同参与零件生产，已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%．按此测算，恰好提前两天完成24000个零件的生产任务，求原计划安排的工人人数．

查看试题解析
27. 已知：在△ABC中，AC=BC，∠ACB=90°，点D是AB的中点，点E是AB边上一点．

(1)、直线BF垂直于直线CE于点F，交CD于点G（如图1），求证：AE=CG；

(2)、直线AH垂直于直线CE，垂足为点H，交CD的延长线于点M（如图2），找出图中与BE相等的线段，并证明．

查看试题解析