广东省湛江市廉江市2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-10-09 类型:期末考试
一、单选题
-
1. 下列四个图案中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各式从左到右的变形正确的是( )A、 B、 C、 D、3. 若a+b=6,ab=4,则a2+4ab+b2的值为( )A、40 B、44 C、48 D、524. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )
2. 下列各式从左到右的变形正确的是( )A、 B、 C、 D、3. 若a+b=6,ab=4,则a2+4ab+b2的值为( )A、40 B、44 C、48 D、524. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( ) A、角的内部到角的两边的距离相等的点在角的平分线上 B、角平分线上的点到这个角两边的距离相等 C、三角形三条角平分线的交点到三条边的距离相等 D、以上均不符合题意5. 分式方程 的解是( )A、4 B、2 C、1 D、-26. 若多项式 = ,则a,b的值分别是( )A、 , B、 , C、 , D、 ,7. 若式子 的值等于0,则x的值为( )A、±2 B、-2 C、2 D、-48. 已知等腰三角形 的底边 ,且 ,则腰 长为( )A、4或12 B、12 C、4 D、8或129. 施工队要铺设一段全长2000米的管道,因在中考期间需停工两天,实际每天施工需比原来计划多50米,才能按时完成任务,求原计划每天施工多少米.设原计划每天施工x米,则根据题意所列方程正确的是( )A、 B、 C、 D、10. 在4×4的正方形网格中,以格点为顶点的三角形称为格点三角形,在图中画出与△ABC关于某条直线对称的格点三角形,最多能画( )个.
A、角的内部到角的两边的距离相等的点在角的平分线上 B、角平分线上的点到这个角两边的距离相等 C、三角形三条角平分线的交点到三条边的距离相等 D、以上均不符合题意5. 分式方程 的解是( )A、4 B、2 C、1 D、-26. 若多项式 = ,则a,b的值分别是( )A、 , B、 , C、 , D、 ,7. 若式子 的值等于0,则x的值为( )A、±2 B、-2 C、2 D、-48. 已知等腰三角形 的底边 ,且 ,则腰 长为( )A、4或12 B、12 C、4 D、8或129. 施工队要铺设一段全长2000米的管道,因在中考期间需停工两天,实际每天施工需比原来计划多50米,才能按时完成任务,求原计划每天施工多少米.设原计划每天施工x米,则根据题意所列方程正确的是( )A、 B、 C、 D、10. 在4×4的正方形网格中,以格点为顶点的三角形称为格点三角形,在图中画出与△ABC关于某条直线对称的格点三角形,最多能画( )个.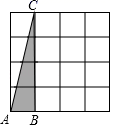 A、5 B、6 C、7 D、8
A、5 B、6 C、7 D、8二、填空题
-
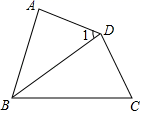
11. 如图, 平分 , , , ,所以 是三角形.
 12. 若正多边形的一个外角是45°,则该正多边形的边数是 .13. 小敏设计了一种衣架,如图,在使用时能轻易收拢,然后套进衣服后松开即可,衣架杆 ,若衣架收拢时, ,则 、 的距离为 .
12. 若正多边形的一个外角是45°,则该正多边形的边数是 .13. 小敏设计了一种衣架,如图,在使用时能轻易收拢,然后套进衣服后松开即可,衣架杆 ,若衣架收拢时, ,则 、 的距离为 .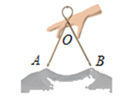 14. 分解因式得 .15. 化简 的结果是 .
14. 分解因式得 .15. 化简 的结果是 .
16. 如图,∠A=30°,∠C'=60°,△ABC与△A’B'C '关于直线l对称,则∠B=.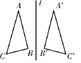 17. 如图,点A在线段DE上,AB⊥AC,垂足为A,且AB=AC,BD⊥DE,CE⊥DE,垂足分别为D、E,若ED=12,BD=8,则CE长为 .
17. 如图,点A在线段DE上,AB⊥AC,垂足为A,且AB=AC,BD⊥DE,CE⊥DE,垂足分别为D、E,若ED=12,BD=8,则CE长为 . 18. 因式分解: .
18. 因式分解: .三、解答题
-
19. 解方程: .20. 如图,每个小正方形的边长均为1,点A和点B在小正方形的格点上.
 (1)、在图①中画出 , 使为直角三角形(要求点C在小正方形的格点上,画一个即可).(2)、求图①中的面积.21. 老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,如下所示:
(1)、在图①中画出 , 使为直角三角形(要求点C在小正方形的格点上,画一个即可).(2)、求图①中的面积.21. 老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,如下所示: (1)、求所捂住的多项式;(2)、若 , 求所捂住多项式的值.22. 某县在“城乡公交一体化改造项目”中,某工程队承接了6千米地下管廊铺设任务,为了赶在年底前完成,实际每天的工作效率比原计划提高20%,结果提前20天完成了任务,问实际每天铺设管廊多少米.23. 如图,AB=AC,CD∥AB,点E是AC上一点,且∠ABE=∠CAD,延长BE交AD于点F.
(1)、求所捂住的多项式;(2)、若 , 求所捂住多项式的值.22. 某县在“城乡公交一体化改造项目”中,某工程队承接了6千米地下管廊铺设任务,为了赶在年底前完成,实际每天的工作效率比原计划提高20%,结果提前20天完成了任务,问实际每天铺设管廊多少米.23. 如图,AB=AC,CD∥AB,点E是AC上一点,且∠ABE=∠CAD,延长BE交AD于点F. (1)、求证:△ABE≌△CAD;(2)、如果∠ABC=65°,∠ABE=25°,求∠D的度数.
(1)、求证:△ABE≌△CAD;(2)、如果∠ABC=65°,∠ABE=25°,求∠D的度数.
