广东省汕头市龙湖区2021-2022学年八年级上学期期末考试数学试题

试卷更新日期：2022-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列长度的三条线段，能组成三角形的是（）

A、3，4，8 B、5，6，10 C、5，5，11 D、5，6，11

查看试题解析
2. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
3. 代数式 $\frac{x}{x + 1}$ ， $\frac{5}{2} x$ ， $\frac{3 x^{3}}{x}$ ， $\frac{x}{π}$ ， $4 - \frac{1}{x}$ 中，分式的个数是（）

A、4 B、3 C、2 D、1

查看试题解析
4. 如图，小明书上的三角形被墨迹遮挡了一部分，但他很快想办法在作业本画了一样的三角形，那么这两个三角形完全一样的依据是（）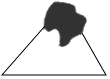

A、AAS B、ASA C、SSS D、SAS

查看试题解析
5. 要使分式 $\frac{3}{x - 2}$ 有意义，则x的取值范围是（）

A、x>2； B、x<2； C、 $x \neq - 2$ ； D、 $x \neq 2$ ；

查看试题解析
6. 如图，△ABC中， $∠ A C B = 90 °$ ，沿CD折叠△CBD，使点B恰好落在AC边上的点E处．若 $∠ A = 22 °$ ，则 $∠ E D A$ 等于（）

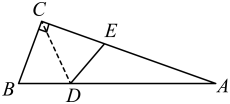A、46° B、56° C、36° D、77°

查看试题解析
7. 下列计算正确的是（）

A、 $a^{5} + a^{5} = a^{10}$ B、 $a^{6} \cdot a^{4} = a^{24}$ C、 $a^{0} = 1$ D、 $(a^{5})^{5} = a^{25}$

查看试题解析
8. 如图，在△ABC和△DEF中，已有条件AB=DE，还需要添加两个条件才能使△ABC≌△DEF，不能添加的一组条件是（）

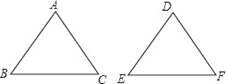A、∠B=∠E，BC=EF B、∠A=∠D，BC=EF C、∠A=∠D，∠B=∠E D、BC=EF，AC=DF

查看试题解析
9. 一个多边形的每个内角都等于135°，则这个多边形的边数为（）

A、8 B、9 C、10 D、11

查看试题解析
10. 如图所示，在△ABC中，∠A=60°，AB=AC，BD是△ABC的角平分线，延长BC至E，使CE=CD，若△ABC的周长为20，BD=a，则△DBE的周长是（）（用含a的式子表示）

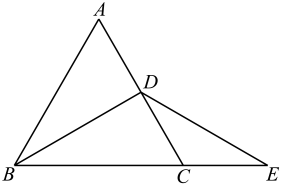A、10+2a B、15+2a C、20+a D、10+a

查看试题解析

二、填空题

11. 已知点M(﹣6，2)，则M点关于x轴对称点的坐标是.

查看试题解析
12. 空调安装在墙上时，一般都会采用如图所示的方法固定，这种方法应用的几何原理是.

查看试题解析
13. 因式分解：2m³﹣2m＝.

查看试题解析
14. 新冠病毒平均直径为0.0001毫米，但它以飞沫传播为主，而飞沫的直径是大于5微米的，所以N95或医用口罩能起到防护作用，用科学记数法表示0.0001是.

查看试题解析
15. 若分式 $\frac{| x | - 2}{x - 2}$ 的值为0，则x＝．

查看试题解析
16. 若关于x的二次三项式 $x^{2} + k x + 36$ 是一个完全平方式，则k= ．

查看试题解析
17. 如图，已知△ABC的周长是16，OB、OC分别平分∠ABC和∠ACB，OD⊥BC于D且OD=2，△ABC的面积是.

查看试题解析

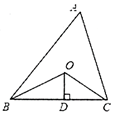
三、解答题

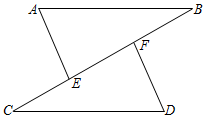
18. 计算：(2x＋5y)(3x－2y)－2x(x－3y)

查看试题解析
19. 如图，点C、E、F、B在同一直线上，AB∥CD，CE＝BF，∠A＝∠D．求证：AB＝CD．

查看试题解析
20. 如图，△ABC中，∠C=90°，∠A=30°．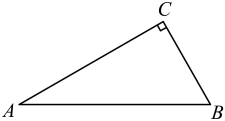

(1)、用尺规作图作∠CBA的角平分线BD，交AC于点D(保留作图痕迹，不要求写作法和证明)；

(2)、在上图中，若BD=10cm，求DC的长

查看试题解析
21. 先化简，再求值： $\frac{x + 1}{x^{2} - 1} \div \frac{x^{2} - x}{x^{2} - 2 x + 1} - \frac{1}{x - 1}$ ，其中x=－2．

查看试题解析
22. 一项工程，甲，乙两公司合做，12天可以完成，共需付施工费102000元；如果甲，乙两公司单独完成此项工程，乙公司所用时间是甲公司的1.5倍，乙公司每天的施工费比甲公司每天的施工费少1500元．

(1)、甲，乙两公司单独完成此项工程，各需多少天？

(2)、若让一个公司单独完成这项工程，哪个公司的施工费较少？

查看试题解析
23. 如图，在△ABC中，已知AB=AC，AB的垂直平分线交AB于点N，交AC于点M，连接MB

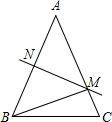(1)、若∠ABC=65°，则∠NMA的度数为

(2)、若AB=10cm，△MBC的周长是18cm
①求BC的长度
②若点P为直线MN上一点，则△PBC周长的最小值为 ▲ cm

查看试题解析
24. 图a是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，再按图b的形状拼成一个正方形.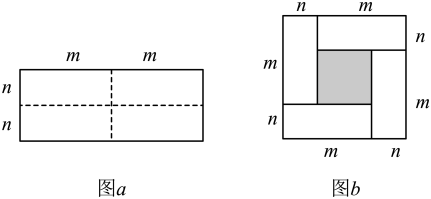

(1)、请用两种不同的方法表示图b中阴影部分的面积
方法1：；方法2：.

(2)、观察图b，写出下面三个式子 $（ m + n ）^{2}$ ， $（ m - n ）^{2}$ ， $m n$ 之间的等量关系；

(3)、根据(2)中的等量关系，解决以下问题：
①已知 $a - b = 5$ ， $a b = - 6$ ，则 $a + b =$ ▲ ；
②已知 $a ＞ 0$ ， $a - \frac{2}{a} = 1$ ，求 $a + \frac{2}{a}$ 的值．(写出解答过程)

查看试题解析
25. 已知，如图1，在平面直角坐标系中，点A、B分别在x轴、y轴的正半轴上，点C在第一象限， $∠ A C B = 90 °$ ， AC=BC，点A的坐标为(m，0)，点C的横坐标为n，且 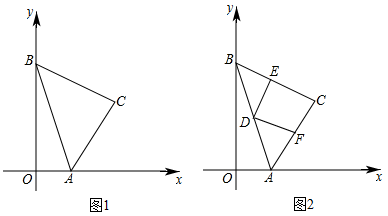$m^{2} + n^{2} - 2 m - 8 n + 17 = 0$ ．

(1)、直接写出m，n的值；

(2)、如图2，D为边AB的中点，以点D为顶点的直角∠EDF的两边分别交边BC于E，交边AC于F
①求证：DE=DF；

②求证： $S_{四边形 D E C F} = \frac{1}{2} S_{△ A B C}$ ；

(3)、在平面坐标内有点G(点G不与点A重合)，使得△BCG是以BC为直角边的等腰直角三角形，请直接写出满足条件的点G的坐标．

查看试题解析