广东省清远市2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列计算中，正确的是（）

A、 $5 \sqrt{7} - 2 \sqrt{7} = 21$ B、 $2 + \sqrt{2} = 2 \sqrt{2}$ C、 $\sqrt{3} \times \sqrt{6} = 3 \sqrt{2}$ D、 $\sqrt{15} \div \sqrt{5} = 3$

查看试题解析
2. 已知平面直角坐标系中点A、B、C、D的坐标如下，位于第二象限的点是（）

A、（1，9） B、（－1，－9） C、（－1，9） D、（1，－9）

查看试题解析
3. 能说明命题“若x为无理数，则x²也是无理数”是假命题的反例是（）

A、 $x = \sqrt{2} - 1$ B、 $x = \sqrt{2} + 1$ C、 $x = 3 \sqrt{2}$ D、 $x = \sqrt{3} - \sqrt{2}$

查看试题解析
4. 已知 $43^{2} = 1849 ， 44^{2} = 1936 ， 45^{2} = 2025 ， 46^{2} = 2116$ ．若 $n$ 为整数且 $n < \sqrt{2021} < n + 1$ ，则 $n$ 的值为（）

A、43 B、44 C、45 D、46

查看试题解析
5. 四盏灯笼的位置如图．已知A，B，C，D的坐标分别是（﹣1，b），（1，b），（2，b），（3.5，b），移动y轴右侧的一盏灯笼，使得y轴两侧的灯笼对称，则移动的方法可以是（）

A、将B移到（－2，b） B、将B移到（－3.5，b） C、将C移到（－2，b） D、将D移到（－2，b）

查看试题解析
6. 下列函数关系式中，属于一次函数的是（）

A、y＝ $\frac{1}{x}$ －1 B、y＝x²＋1 C、y＝kx＋b（k、b是常数） D、y＝1－2x

查看试题解析
7. 在学校举办的学习强国演讲比赛中，李华根据九位评委所给的分数制作了如下表格：
平均数
中位数
众数
方差
8.5
8.3
8.1
0.15
如果去掉一个最高分和一个最低分，则表中数据一定不发生变化的是（　　）

A、平均数 B、众数 C、方差 D、中位数

查看试题解析
8. 函数y＝ax＋b与函数y＝cx＋d的图象是两条相交直线，则二元一次方程组 ${\begin{array}{l} y = a x + b \\ y = c x + d \end{array}$ 有（）解．

A、0个 B、1个 C、2个 D、3个

查看试题解析
9. 如图，小华将升旗的绳子拉紧到旗杆底端点B，绳子末端刚好接触到地面，然后拉紧绳子使其末端到点D处，点D到地面的距离CD长为2m，点D到旗杆AB的水平距离为8m，若设旗杆的高度AB长为xm，则根据题意所列的方程是（）．

A、 ${(x - 2)}^{2} + 8^{2} = x^{2}$ B、 ${(x + 2)}^{2} + 8^{2} = x^{2}$ C、 $x^{2} + 8^{2} = {(x - 2)}^{2}$ D、 $x^{2} + 8^{2} = {(x + 2)}^{2}$

查看试题解析
10. 对于一次函数y＝﹣2x+4，下列结论中正确的是（）

A、函数值随自变量的增大而增大 B、点(4﹣a，a)在该函数的图象上 C、函数的图象与直线y＝﹣x﹣2平行 D、函数图象与坐标轴围成三角形的周长为6+2 $\sqrt{5}$

查看试题解析

二、填空题

11. 平面直角坐标系中，用横坐标表示电影票上的“排号”，纵坐标表示“座号”，则电影票上“3排6座”可表示为．

查看试题解析
12. 若 $\sqrt{x - 7}$ 在实数范围内有意义，则实数 $x$ 的取值范围是．

查看试题解析
13. 有甲､乙两组数据，如表所示：

甲

11

12

13

14

15

乙

12

12

13

14

14

甲､乙两组数据的方差分别为 $s_{甲}^{2}, s_{乙}^{2}$ ，则 $s_{甲}^{2}$ $s_{乙}^{2}$ （填“＞”，“＜”或“＝”）．

查看试题解析
14. 已知 $\sqrt{2 a + 2} + | b - \sqrt{3} | = 0$ ，则ab＝．

查看试题解析
15. 将一副直角三角板如图放置，使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合，则∠1的大小为度．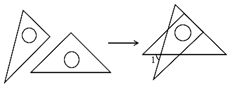

查看试题解析
16. 如图，OP＝1，过点 P 作 PP₁⊥OP 且 PP₁＝1，得 OP₁＝ $\sqrt{2}$ ；再过点 P₁作 P₁P₂⊥OP₁且 P₁P₂＝1，得 OP₂＝ $\sqrt{3}$ ；又过点 P₂作 P₂P₃⊥OP₂且 P₂P₃＝1，得 OP₃＝2；…依此法继续作下去，得 OP₂₀₂₁＝．

查看试题解析
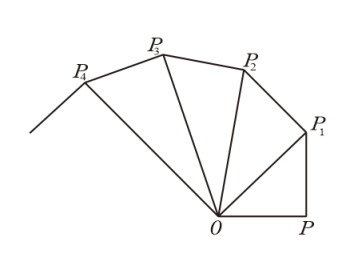17. 如图，在平面直角坐标系中，直线y＝x＋2交x轴于点A，交y轴于点A₁ ，若图中阴影部分的三角形都是等腰直角三角形，则从左往右第3个阴影三角形的面积是，第n个阴影三角形的面积是．

查看试题解析

三、解答题

18. 计算： $\sqrt[3]{27} + （ - 3 ）^{0} - \sqrt{8} + | - 2 \sqrt{2} |$

查看试题解析
19. 解方程组： ${\begin{matrix} x = 2 y \\ x - y = 6 \end{matrix}$ ．

查看试题解析
20. 为了推进中华传统文化教育，营造浓郁的读书氛围，某初中举办了“建设书香校园”主题活动．为此特为每个班级订购了一批新的图书．初一年级两个班订购图书情况如下表：

老舍文集（套）
四大名著（套）
总费用（元）
初一（1）班
6
4
860
初一（2）班
5
4
800
求老舍文集和四大名著每套各是多少元？

查看试题解析
21. 如图所示，△ABC的顶点A、B、C在边长为1的正方形网格的格点上，BD⊥AC于点D，

(1)、求BD的长；

(2)、请在图中以B为原点，BC边为x轴建立平面直角坐标系，并写出A、B、C的坐标．

查看试题解析
22. 生物学研究表明，某种蛇的长度y（cm）是其尾长x（cm）的一次函数．当蛇的尾长为6cm时，蛇长为45.5cm；当尾长为14cm时，蛇长为105.5cm．

(1)、写出x，y之间的关系式；

(2)、当一条蛇的尾长为10cm时，这条蛇的长度是多少？

查看试题解析
23. 如图，有一艘货船和一艘客船同时从港口A出发，客船每小时比货船多走5海里，客船与货船速度的比为4：3，货船沿东偏南10°方向航行，2小时后货船到达B处，客船到达C处，若此时两船相距50海里.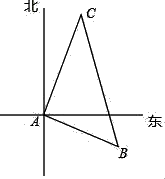

(1)、求两船的速度分别是多少？

(2)、求客船航行的方向.

查看试题解析
24. 李师傅将容量为60升的货车油箱加满后，从工厂出发运送一批物资到某地．行驶过程中，货车离目的地的路程s（千米）与行驶时间t（小时）的关系如图所示（中途休息、加油的时间不计．当油箱中剩余油量为10升时，货车会自动显示加油提醒．设货车平均耗油量为0.1升/千米，请根据图象解答下列问题：

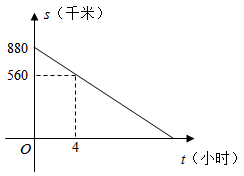(1)、直接写出工厂离目的地的路程；

(2)、求s关于t的函数表达式；

(3)、当货车显示加油提醒后，问行驶时间t在怎样的范围内货车应进站加油？

查看试题解析
25. [探究]如图①所示， $∠ A F H$ 和 $∠ C H F$ 的平分线交于点O， $E G$ 经过点O且平行于 $F H$ ，分别与 $A B$ 、 $C D$ 交于点E、G．

(1)、若 $∠ A F H = 60 °$ ， $∠ C H F = 50 °$ ，则 $∠ E O F =$ $°$ ， $∠ F O H =$ $°$ ；

(2)、若 $∠ A F H + ∠ C H F = 100 °$ ，求 $∠ F O H$ 的度数．

(3)、 [拓展]如图②所示， $∠ A F H$ 和 $∠ C H I$ 的平分线交于点O， $E G$ 经过点O且平行于 $F H$ ，分别与 $A B$ 、 $C D$ 交于点E、G．若 $∠ A F H + ∠ C H F = α$ ，直接写出 $∠ F O H$ 的度数．（用含 $α$ 的代数式表示）

查看试题解析

	老舍文集（套）	四大名著（套）	总费用（元）
初一（1）班	6	4	860
初一（2）班	5	4	800

平均数	中位数	众数	方差
8.5	8.3	8.1	0.15

甲	11	12	13	14	15
乙	12	12	13	14	14