广东省梅州市平远县2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列是无理数的是（）

A、 $\frac{1}{2}$ B、3 C、 $π$ D、－2.6

查看试题解析
2. 在某个电影院里，如果用(3，13)表示3排13号，那么2排6号可以表示为（）

A、(3，6) B、(13，6) C、(6，2) D、(2，6)

查看试题解析
3. 若 $x^{3 m - 2} - 2 y^{n - 1} = 5$ 是二元一次方程，则 $m + n =$ （）．

A、1 B、2 C、3 D、1或2

查看试题解析
4. 已知一组数据：2，0，-1，4，2，-3．这组数据的众数和中位数分别是（）

A、2，1.5 B、2，-1 C、2，1 D、2，2

查看试题解析
5. 若关于x的函数y=2x+a是正比例函数，则a的值是（）

A、0 B、1 C、2 D、3

查看试题解析
6. 下列命题中错误的是（）

A、一组数据4，5，x，7，9的平均数为6，则x为5 B、两直线平行，同旁内角互补 C、 $3^{2}$ 、 $4^{2}$ 、 $5^{2}$ 能作为直角三角形的三边长 D、估算 $\sqrt{10} - 1$ 的值在2和3之间

查看试题解析
7. 若点A(1，2)，B(-1，2)，则点A与点B的关系是（）

A、关于x轴对称 B、关于y轴对称 C、关于直线x=1对称 D、关于直线y=1对称

查看试题解析
8. 若点A（ $x_{1}$ ，－1），B（ $x_{2}$ ，－3），C（ $x_{3}$ ， 4）在一次函数y＝－2x＋m（m是常数）的图象上，则 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 的大小关系是（）

A、 $x_{1}$ ＞ $x_{2}$ ＞ $x_{3}$ B、 $x_{2}$ ＞ $x_{1}$ ＞ $x_{3}$ C、 $x_{1}$ ＞ $x_{3}$ ＞ $x_{2}$ D、 $x_{3}$ ＞ $x_{2}$ ＞ $x_{1}$

查看试题解析
9. 如图，分别以 $Rt △ ABC$ 的三边为斜边向外作等腰直角三角形，若斜边 $A B = 6$ ，则图中阴影部分的面积为（）．

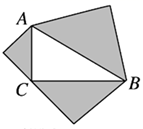A、6 B、12 C、16 D、18

查看试题解析
10. 已知关于x，y的方程组 ${\begin{array}{l} 2 x - y = 5 \\ a x + b y = 2 \end{array}$ 和 ${\begin{array}{l} x + y = 4 \\ a x + 2 b y = 10 \end{array}$ 有相同的解，那么 $a + b$ 值是（）

A、5 B、4 C、3 D、6

查看试题解析

二、填空题

11. 若数x－2的平方根只有一个，则x的值是．

查看试题解析
12. 如图，将一副直角三角板按图中所示位置摆放，保持AB∥DE，则∠ACD的度数为．

查看试题解析
13. 在平面直角坐标系中，点A在x轴上，且到原点的距离是 $\sqrt{6}$ ，则点A的坐标是．

查看试题解析
14. 甲、乙两位同学进行打字比赛，各自录入同一篇800字的文章，两人在比赛开始后前五分钟打字速度（单位：个/分钟）的折线统计图如图，则每分钟打字速度更稳定的是（填“甲”或“乙”）同学.

查看试题解析
15. 小明在解题时发现二元一次方程□ $x - y = 3$ 中， $x$ 的系数已经模糊不清（用“□”表示），但查看答案发现 ${\begin{array}{l} x = - 2 \\ y = 5 \end{array}$ 是这个方程的一组解，则□表示的数为.

查看试题解析
16. 已知一次函数 $y = k x - b$ （k、b为常数，且 $k \neq 0$ ， $b \neq 0$ ）与 $y = \frac{1}{3} x$ 的图象相交于点 $M (a ， \frac{1}{2})$ ，则关于x的方程 $(k - \frac{1}{3}) x = b$ 的解为 $x =$ ．

查看试题解析
17. 如图所示，ABCD是长方形地面，长AB＝20m，宽AD＝10m．中间竖有一堵砖墙高MN＝2m．一只蚂蚱从A点爬到C点，它必须翻过中间那堵墙，则它至少要走的路程．

查看试题解析

三、解答题

18. 计算： $- (\sqrt{2} - 1)^{0} + \sqrt{48} \div \sqrt{3} - \sqrt{\frac{1}{2}} \times \sqrt{24} - \sqrt[3]{27}$ ．

查看试题解析
19. 已知关于 $x$ ， $y$ 的二元一次方程组 ${\begin{array}{l} 2 x + y = 4 \\ 4 x + 3 y = 2 m + 2 \end{array}$ 的解满足 $x + y = 2$ ，求实数 $m$ 的值.

查看试题解析
20. 小明和朋友到人民公园游玩，回到家后，利用平面直角坐标系画出了公园的景区地图，如图所示．可是他忘记了在图中标出原点和x轴、y轴，只知道游乐园D的坐标为(1，﹣3)，请你帮他画出平面直角坐标系，并写出其他各景点的坐标．

查看试题解析
21. 已知：∠AOB＝ $α$ （0°＜ $α$ ＜90°），一块三角板CDE中，∠CED＝90°，∠CDE＝30°，将三角板CDE如图所示放置，使顶点C落在OB边上，经过点D作直线MN∥OB交OA边于点M，且点M在点D的左侧．

(1)、如图1，若CE∥OA，EF∥MN，∠NDE＝45°，求 $α$ 的度数；

(2)、若∠MDC的平分线DF交OB边于点F，如图2，当DF∥OA，且 $α$ ＝60°时，证明：CE∥OA．

查看试题解析
22. 梅州金柚，声名远播，今年又是一个丰收年．某经销商为了打开销路，对1000个金柚进行打包优惠出售．打包方式及售价如图．假设用这两种打包方式恰好完全部柚子．当销售总收入为7280元时．

(1)、若这批金全部售完，请问纸盒装共包装了多少箱，编织袋装共包装了多少袋？

(2)、若该经销商留下b（b＞0）箱纸盒装送人，其余纸盒装全部售出，求b的值．

查看试题解析
23. 校学生会向全校3000名学生发起了“爱心捐助”捐款活动，为了解捐款情况，学生会随机绘制了如图的统计图．请根据相关信息，解答下列问题：

(1)、本次接受随机调查的学生人数为，图1中m的值是；

(2)、求本次调查获取的样本数据的平均数、众数和中位数；

(3)、根据样本数据，估计该校本次活动捐款金额为10元的学生人数．

查看试题解析
24. 如图，在△ABC中，AB＝AC．

(1)、若P为BC上的中点，求证： $A B^{2} - A P^{2} = P B \cdot P C$ ；

(2)、若P为线段BC上的任意一点，（1）中的结论是否成立，并证明；

(3)、若P为BC延长线上一点，说明AB、AP、PB、PC之间的数量关系．

查看试题解析
25. 如图，在平面直角坐标系中，函数 $y = - x + 2$ 的图象与x轴，y轴分别交于点A，B，与函数 $y = \frac{1}{3} x + b$ 的图象交于点 $C (- 2 ， m)$ ．

(1)、求m和b的值；

(2)、函数 $y = \frac{1}{3} x + b$ 的图象与x轴交于点D，点E从点D出发沿DA方向，以每秒2个单位长度匀速运动到点A（到A停止运动）．设点E的运动时间为t秒．
①当 $△ A C E$ 的面积为12时，求t的值；
②在点E运动过程中，是否存在t的值，使 $△ A C E$ 为直角三角形？若存在，请求出t的值；若不存在，请说明理由．

查看试题解析