广东省茂名市高州市2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-10-09 类型:期末考试
一、单选题
-
1. 下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、2. 若点M(a,﹣1)与点N(2,b)关于x轴对称,则a+b的值是( )A、1 B、﹣1 C、3 D、﹣33. 在函数中,自变量x的取值范围是( )A、 B、 C、 D、4. 如图所示,直线a∥b, , ,则 ( )
 A、32︒ B、78︒ C、22︒ D、20︒5. 某校开展阅读经典活动,小明3天里阅读的总页数比小颗5天里阅读的总页数少6页,小颖平均每天阅读的页数比小明平均每天阅读的页数的2倍少10页,若小明、小颖平均每天分别阅读x页、y页,则下列方程组正确的是( )A、 B、 C、 D、6. 高州市是广东省省辖县级市,自古以来便是一个人杰地灵,经济文化繁荣昌盛的粤西重镇,史称潘州,以下能准确表示高州市地理位置的是( )A、在广州的西南方 B、东经110°,北纬22° C、距离广州350公里处 D、东经110°7. 设面积为3的正方形的边长为x,那么关于x的说法正确的是( )A、x是有理数 B、x取0和1之间的实数 C、x不存在 D、x取1和2之间的实数8. 国庆节期间,重庆南开中学用彩灯带装饰了艺术楼大厅的所有圆柱形柱子.为了美观,每根柱子的彩灯带需要从月点沿柱子表面缠绕两周到其正上方的3点,如图所示.若每根柱子的底面周长均为2米,高均为3米,则每根柱子所用彩灯带的最短长度为( )
A、32︒ B、78︒ C、22︒ D、20︒5. 某校开展阅读经典活动,小明3天里阅读的总页数比小颗5天里阅读的总页数少6页,小颖平均每天阅读的页数比小明平均每天阅读的页数的2倍少10页,若小明、小颖平均每天分别阅读x页、y页,则下列方程组正确的是( )A、 B、 C、 D、6. 高州市是广东省省辖县级市,自古以来便是一个人杰地灵,经济文化繁荣昌盛的粤西重镇,史称潘州,以下能准确表示高州市地理位置的是( )A、在广州的西南方 B、东经110°,北纬22° C、距离广州350公里处 D、东经110°7. 设面积为3的正方形的边长为x,那么关于x的说法正确的是( )A、x是有理数 B、x取0和1之间的实数 C、x不存在 D、x取1和2之间的实数8. 国庆节期间,重庆南开中学用彩灯带装饰了艺术楼大厅的所有圆柱形柱子.为了美观,每根柱子的彩灯带需要从月点沿柱子表面缠绕两周到其正上方的3点,如图所示.若每根柱子的底面周长均为2米,高均为3米,则每根柱子所用彩灯带的最短长度为( ) A、米 B、米 C、米 D、5米9. 已知一次函数中y随x的增大而减小,且 , 则在直角坐标系内它的大致图象是( )A、
A、米 B、米 C、米 D、5米9. 已知一次函数中y随x的增大而减小,且 , 则在直角坐标系内它的大致图象是( )A、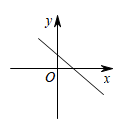 B、
B、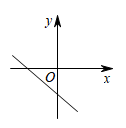 C、
C、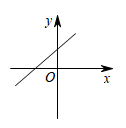 D、
D、 10. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于点E,交AC于点F,过点O作OD⊥AC于点D,下列四个结论:①BE=EF﹣CF;②∠BOC=90°+∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S△AEF=mn,其中正确结论的个数有( )
10. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于点E,交AC于点F,过点O作OD⊥AC于点D,下列四个结论:①BE=EF﹣CF;②∠BOC=90°+∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S△AEF=mn,其中正确结论的个数有( )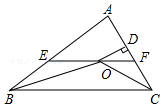 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 的立方根是 .12. 一个正数的两个平方根分别为和 , 则a的值为 .13. 已知一次函数y=﹣2x+4图象上两点(﹣1,y1),(3,y2),则y1y2(填“>”、“<”或“=”).14. 如图,D为△ABC边AC上一点,以点A为圆心,AD为半径画弧,交BA的延长线于点E,连接ED.若∠B=60°,∠C=70°,则∠ADE的度数为 .
 15. 已知 是关于x,y的二元一次方程,则 .16. 若方程 有两个解 和 ,则 的值为 .17. 某学校创客小组进行机器人跑步大赛,机器人小 和小 从同一地点同时出发,小 在跑到1分钟的时候监控到程序有问题,随即开始进行远程调试,到3分钟的时候调试完毕并加速前进,最终率先到达终点,测控小组记录的两个机器人行进的路程与时间的关系如图所示,则以下结论正确的有(填序号).
15. 已知 是关于x,y的二元一次方程,则 .16. 若方程 有两个解 和 ,则 的值为 .17. 某学校创客小组进行机器人跑步大赛,机器人小 和小 从同一地点同时出发,小 在跑到1分钟的时候监控到程序有问题,随即开始进行远程调试,到3分钟的时候调试完毕并加速前进,最终率先到达终点,测控小组记录的两个机器人行进的路程与时间的关系如图所示,则以下结论正确的有(填序号).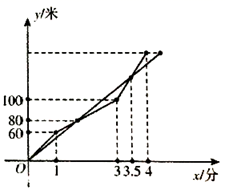
①两个机器人第一次相遇时间是在第2分钟;
②小 每分钟跑50米;
③赛程总长200米;
④小 到达终点的时候小 距离终点还有20米.
三、解答题
-
18. 计算: .19. 解二元一次方程组: .20. 在下列网格中建立平面直角坐标系如图,每个小正方形的边长均为1个单位长度.已知A(1,1),B(3,5)和C(4,2).
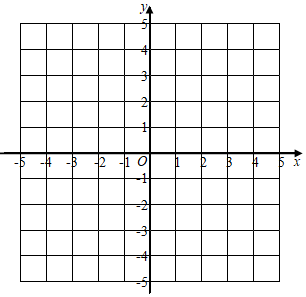
( 1 )在图中标出点A、B、C.并画出△ABC;
( 2 )画出△ABC关于y轴对称的图形△A1B1C1 .
( 3 )求△ABC的面积.
21. 某学校从八年级同学中任意选取40人,随机分成甲、乙两个小组进行“引体向上”体能测试.根据测试成绩绘制出下面的统计表和如图的统计图.已知甲组的平均成绩为8.7分.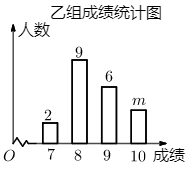
甲组成绩统计表:
成绩
7
8
9
10
人数
1
9
5
5
请根据上面的信息,解答下列问题:
(1)、m= , 甲组成绩的中位数是 , 乙组成绩的众数是;(2)、参考下面甲组成绩方差的计算过程,求乙组成绩的方差,并判断哪个小组的成绩更加稳定?22. 如图,在平面直角坐标系中,直线y=−2x+12与x轴交于点A,与y轴交于点B,与直线y=x交于点C. (1)、求点C的坐标.(2)、若P是x轴上的一个动点,直接写出当△POC是等腰三角形时P的坐标.(3)、在直线AB上是否存在点M,使得△MOC的面积是△AOC面积的2倍?若存在,请求出点M的坐标;若不存在,请说明理由.23. 如图,CB为∠ACE的平分线,F是线段CB上一点,CA=CF,∠B=∠E,延长EF与线段AC相交于点D.
(1)、求点C的坐标.(2)、若P是x轴上的一个动点,直接写出当△POC是等腰三角形时P的坐标.(3)、在直线AB上是否存在点M,使得△MOC的面积是△AOC面积的2倍?若存在,请求出点M的坐标;若不存在,请说明理由.23. 如图,CB为∠ACE的平分线,F是线段CB上一点,CA=CF,∠B=∠E,延长EF与线段AC相交于点D.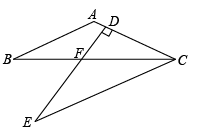 (1)、求证:AB=FE;(2)、若ED⊥AC,ABCE,求∠A的度数.24. 某大酒店客房部有三人间、双人间和单人间客房,收费数据如下表(例如三人间普通间客房每人每天收费50元).为吸引客源,在“元旦”期间进行优惠大酬宾,凡团体入住一律五折优惠,一个50人的旅游团在十二月三十一号到该酒店住宿,租住了一些三人间、双人间普通客房.
(1)、求证:AB=FE;(2)、若ED⊥AC,ABCE,求∠A的度数.24. 某大酒店客房部有三人间、双人间和单人间客房,收费数据如下表(例如三人间普通间客房每人每天收费50元).为吸引客源,在“元旦”期间进行优惠大酬宾,凡团体入住一律五折优惠,一个50人的旅游团在十二月三十一号到该酒店住宿,租住了一些三人间、双人间普通客房.普通间(元/人/天)
豪华间(元/人/天)
贵宾间(元/人/天)
三人间
50
100
500
双人间
70
150
800
单人间
100
200
1500
(1)、如果每个客房正好住满,一天共需住宿费1510元,求三人间、双人间普通客房各住了多少间?(2)、设三人间共住了x人,且按实际占用的床位收费,一天的住宿费用y元表示,写出y与x的函数关系式;(3)、为了方便管理,酒店规定不同旅行团的成员不得混住到同一间寝室,且收费方式改为按该团占用的寝室个数收费.比如,某旅行团住了一个三人间,但只住了两个旅客,若仍按三人入住收费.如果你是该团领队,你认为(1)中的住宿方式是不是费用最少的?为什么?25. 一些含根号的式子可以写成另一个式子的平方,如3+2=(1+)2 . 设a+b(其中a、b、m、n均为正整数),则有a+b=m2+2n2+2mn , ∴a=m2+2n2 , b=2mn.这样可以把部分a+b的式子化为平方式的方法.请你仿照上述的方法探索并解决下列问题:(1)、当a、b、m、n均为正整数时,若a+b=(m+n)2 , 用含m、n的式子分别表示a、b,得:a= , b= .(2)、利用所探索的结论,找一组正整数a、b、m、n填空:+=(+)2;(3)、化简