广东省江门市台山市2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 生活垃圾处理是关系民生的基础性公益事业，加强生活垃圾管理，维护公共环境和节约资源是全社会共同的责任．下列四个垃圾分类标识中的图形是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 分式 $\frac{x^{2} - 4}{x - 2}$ 的值为0，则（）

A、x＝0 B、x＝﹣2 C、x＝2 D、x＝±2

查看试题解析
3. 点M（3，1）关于y轴的对称点的坐标为（）

A、（﹣3，1） B、（3，﹣1） C、（﹣3．﹣1） D、（1，3）

查看试题解析
4. 若一个多边形的内角和是540°，则该多边形的边数为（）

A、4 B、5 C、6 D、7

查看试题解析
5. 随着人们对环境的重视，新能源的开发迫在眉睫，石墨烯是现在世界上最薄的纳米材料，其理论厚度应是0.0000034 m，用科学记数法表示0.0000034是（）

A、0.34×10^-5 B、3.4×10⁶ C、3.4×10^-5 D、3.4×10^-6

查看试题解析
6. 将一副三角板按图中方式叠放，则角α等于（）

A、30° B、45° C、60° D、75°

查看试题解析
7. 下列运算正确的是（）

A、 $(m + 1) (m - 1) = m^{2} - 1$ B、 ${(- 3 a^{2})}^{2} = 6 a^{4}$ C、 $a^{2} \cdot a^{3} = a^{6}$ D、 $2 a b \cdot (- \frac{1}{2} a b) = - a b$

查看试题解析
8. 随着快递业务的增加，某快递公司为快递员更换了快捷的交通工具，公司投递快件的能力由每周3000件提高到4200件，平均每人每周比原来多投递40件，若快递公司的快递员人数不变，求原来平均每人每周投递快件多少件？设原来平均每人每周投递快件x件，根据题意可列方程为（）

A、 $\frac{3000}{x}$ ＝ $\frac{4200}{x - 40}$ B、 $\frac{3000}{x} + 40 = \frac{4200}{x}$ C、 $\frac{4200}{x}$ ＝ $\frac{3000}{x}$ ﹣40 D、 $\frac{3000}{x}$ ＝ $\frac{4200}{x + 40}$

查看试题解析
9. 如图，在△ABC 和△DEF 中，AC=DF，AB=DE，添加下列一个条件后，仍然不能证明△ABC≌△DEF，这个条件是（）

A、∠A=∠D B、BE=CF C、∠ACB=∠DFE=90° D、∠B=∠DEF

查看试题解析
10. 如图，在四边形ABCD中，∠A＝90°，AD＝6，连接BD，BD⊥CD，∠ADB＝∠C．若P是BC边上一动点，则DP长的最小值为（）

A、4 B、6 C、3 D、12

查看试题解析

二、填空题

11. 当x时，分式 $\frac{3}{2 x + 1}$ 有意义．

查看试题解析
12. 因式分解： $a^{2} - 9 b^{2} =$ ．

查看试题解析
13. 如图，已知 $△ A B D ≌ △ A C E$ ， $∠ A = 53 °$ ， $∠ B = 22 °$ ，则 $∠ A E C =$ °．

查看试题解析
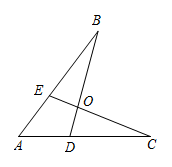14. （3a²﹣6ab）÷3a= ．

查看试题解析
15. 若 $x - y = 3$ ， $x y = 2$ ，则 $x^{2} + y^{2} =$ .

查看试题解析
16. 若一条长为 $24 cm$ 的细线能围成一边长等于 $6 cm$ 的等腰三角形，则该等腰三角形的腰长为cm．

查看试题解析
17. 如图，等腰三角形 $A B C$ 的底边 $B C$ 长为6，面积是36，腰 $A C$ 的垂直平分线 $E F$ 分别交 $A C$ ， $A B$ 边于E，F点，若点D为 $B C$ 边的中点，点M为线段 $E F$ 上一动点，则 $Δ C D M$ 周长的最小值．

查看试题解析

三、解答题

18. 化简： $(3 m + n)^{2} - 3 m (m + n)$ ．

查看试题解析
19. 先化简，再求值： $- \frac{x^{2} - 4}{x^{2} - 4 x + 4} \div \frac{x + 2}{x + 1}$ $+ \frac{x}{x - 2}$ ，其中x＝2﹣ $\sqrt{2}$ ．

查看试题解析
20. 如图，在四边形ABCD中， $∠ B = 90 °$ ， AB//CD，M为 $B C$ 的中点，且 $A M$ 平分 $∠ B A D$ ．求证： $D M$ 平分 $∠ A D C$ ．

查看试题解析
21. 为了帮助湖北省武汉市防控新冠肺炎，某爱心组织筹集了部分资金，计划购买甲、乙两种救灾物资共2000件送往灾区，已知每件甲种物资的价格比每件乙种物资的价格贵10元，用350元购买甲种物资的件数恰好与用300元购买乙种物资的件数相同．

(1)、求甲、乙两种救灾物资每件的价格各是多少元？

(2)、经调查，灾区对甲种物资的需求量不少于乙种物资的1.5倍，该爱心组织共需要购买2000件物资，请问乙种物资最多能购买多少件？

查看试题解析
22. 如图，已知 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 30 °$ ， AC边上的垂直平分线DE交AB于点D，交AC于E．

(1)、 $∠ B C D$ 的度数；

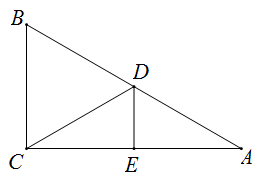(2)、若 $D E = 3$ ，求AB的长．

查看试题解析
23. 如图，AB∥CD，AD与BC相交于点E，AF平分∠BAD，交BC于点F，交CD的延长线于点G.

(1)、若∠G=29°，求∠ADC的度数；

(2)、若点F是BC的中点，求证：AB=AD+CD.

查看试题解析
24. 已知 $(x + a) (x + b) = x^{2} + m x + n$ ．

(1)、若 $a = - 3$ ， $b = 2$ ，则 $m =$ ， $n =$ ；

(2)、若 $m = - 2$ ， $n = \frac{1}{2}$ ，求 $\frac{1}{a} + \frac{1}{b}$ 的值；

(3)、若 $n = - 1$ ，当 $\frac{1}{a^{2}} + 4 a + \frac{1}{b^{2}} + 4 b + 2 = 0$ 时，求m的值．

查看试题解析
25. 如图，在 $△ A B C$ 中， $A B = A C$ ．

(1)、点D是线段 $B C$ 上一点（不与B，C重合），以 $A D$ 为一边在 $A D$ 的右侧作 $△ A D E$ ，使 $A D = A E$ ， $∠ D A E = ∠ B A C$ ，连接 $C E$ ．
①求证： $△ A B D ≌ △ A C E$ ；
②若 $∠ B A C = 48 °$ ，则 $∠ B C E =$ 度；
③猜想 $∠ B A C$ 与 $∠ B C E$ 之间的数量关系，并证明你的结论．

(2)、当点D在线段 $B C$ 的反向延长线上运动时，（1）③中的结论是否仍然成立？若成立，试加以证明；若不成立，请你给出正确的数量关系，并说明理由．

查看试题解析