广东省江门市蓬江区2020-2021学年八年级上学期期末数学试题

试卷更新日期：2022-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下面四幅作品分别代表“立春”、“芒种”、“白露”、“大雪”四个节气，其中轴对称图形是（）

A、 B、 C、 D、

查看试题解析
2. 世界上能制造出的最小晶体管的长度为0.000 000 04米，将0.000 000 04米用科学记数法表示为（）

A、 $4 \times 1 0^{- 8}$ B、 $4 \times 1 0^{- 9}$ C、 $0.4 \times 1 0^{9}$ D、 $40 \times 1 0^{- 7}$

查看试题解析
3. 下列各式中，从左到右的变形是因式分解的是（）

A、 $(x + 1) (x - 1) = x^{2} - 1$ B、 $x^{2} - 4 x + 4 = x (x - 4) + 4$ C、 $(x + 3) (x - 4) = x^{2} - x - 12$ D、 $x^{2} - 4 = (x + 2) (x - 2)$

查看试题解析
4. 使分式 $\frac{x}{x + 2}$ 有意义的 $x$ 的取值范围是（）

A、 $x \neq - 2$ B、 $x \neq 0$ C、 $x > - 2$ D、 $x < - 2$

查看试题解析
5. 下列计算正确的是（）

A、 $(x^{3})^{3} = x^{6}$ B、 $a^{6} \cdot a^{4} = a^{24}$ C、 $3 a + 2 a = 5 a$ D、 $3 a^{2} - 2 a^{2} = a$

查看试题解析
6. 下列选项中最简分式是（）

A、 $\frac{1}{x^{2} + 1}$ B、 $\frac{2}{4 x^{2}}$ C、 $\frac{x + 1}{x^{2} - 1}$ D、 $\frac{3 x^{2} + x}{x}$

查看试题解析
7. 如图，用尺规作图作已知角平分线，其根据是构造两个三形全等，它所用到的判别方法是（）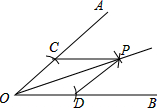

A、SAS B、AAS C、ASA D、SSS

查看试题解析
8. 如图，CE $∥$ BF，AE=DF，要使△EAC≌△FDB．需要添加下列选项中的（）

A、AB=CD B、EC=BF C、∠A=∠D D、AB=BC

查看试题解析
9. 如图，AD是△ABC的角平分线，∠C=28°，AB+BD=AC、将△ABD沿AD所在直线翻折，点B在AC边上的落点记为点E，那么∠AED的度数为（）

A、28° B、50° C、56° D、65°

查看试题解析
10. 对于两个不相等的实数a、b，我们规定符号Min｛a，b｝表示a、b中较小的值，如Min｛2，4｝=2，按照这个规定，方程Min｛ $\frac{1}{x} ， \frac{3}{x}$ ｝= $\frac{4}{x} - 1$ 的解为（）

A、1或3 B、1或-3 C、1 D、3

查看试题解析

二、填空题

11. （-2021）⁰＝．

查看试题解析
12. 点 $A (- 1 ， 2)$ 关于x轴对称点的坐标是．

查看试题解析
13. 已知三角形的两边分别为 $2$ 和 $7$ ，则第三边 $c$ 的取值范围是．

查看试题解析
14. 若 $4^{x} = 6$ ， $4^{y} = 12$ ，则 $4^{2 x - y} =$ ．

查看试题解析
15. 如图，在△ABC中，∠ABC和∠ACB的平分线相交于F点，过点F作DE $∥$ BC，交AB于点D，交AC于点E，若 AB=8，AC=9，则△ADE的周长为．

查看试题解析
16. 如图，已知正五边形ABCDE，AF∥CD，交DB的延长线于点F，则∠DFA＝度.

查看试题解析
17. 如图，∠MON=30°，点 $A_{1} 、 A_{2} 、 A_{3}$ …在射线ON上，点 $B_{1} 、 B_{2} 、 B_{3}$ …在射线OM上，△ $A_{1} B_{1} A_{2}$ ， △ $A_{2} B_{2} A_{3}$ ， △ $A_{3} B_{3} A_{4}$ ， …均为等边三角形，从左数起第1个等边三角形的边长记 $a 1$ ，第2个等边三角形的边长记 $a 2$ ，以此类推，若 $O A_{1}$ =1，则 $a {}_{2021}=$ ．

查看试题解析

三、解答题

18. 计算： $(x - 3)^{2} - x (x - 6)$

查看试题解析
19. 先化简，再求值： $(\frac{1}{x - 2} + \frac{1}{x + 2}) \cdot (x^{2} - 4)$ ，其中 $x = \frac{1}{3}$ ．

查看试题解析
20. 如图，△ABC中，∠B=2∠C，E为BC上一点，且到A、C两点的距离相等．

(1)、尺规作图：作出点 E的位置（保留作图痕迹）；

(2)、连接 AE，求证：AB=AE．

查看试题解析
21. 如图，在 $Δ A B C$ 中，点 $D$ ， $E$ 分别是 $A B$ 、 $A C$ 边上的点， $B D = C E$ ， $∠ A B E = ∠ A C D$ ， $B E$ 与 $C D$ 相交于点 $F$ ，求证： $Δ A B C$ 是等腰三角形．

查看试题解析
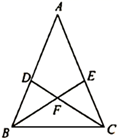22. 如图，两个正方形的边长分别为a、b ，如果a+b=18，ab=70，求图中阴影部分面积．

查看试题解析
23. 山地自行车倍受中学生的喜爱，一网店经营的一个型号山地自行车，今年一月份销售额为27000元，二月份每辆车售价比一月份每辆车售价降价100元，若销售的数量与上一月销售的数量相同，则销售额是24000元．

(1)、求二月份每辆车售价是多少元?

(2)、为了促销，三月份每辆车售价比二月份每辆车售价降低了10%销售，网店仍可获利44%，求每辆山地自行车的进价是多少元?

查看试题解析
24. 如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，以AB为一边向上作等边三角形 ABD，点E在BC垂直平分线上，且EB⊥AB，连接 CE，AE，CD．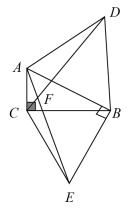

(1)、判断△CBE的形状，并说明理由；

(2)、求证：AE=DC；

(3)、若CD与AE相交于点F，CD与AB相交于点G，求∠AFD的度数．

查看试题解析
25. 如图，△ABC和△AOD是等腰直角三角形，AB=AC，AO=AD，∠BAC=∠OAD=90°，点O是△ABC内的一点，∠BOC=130°．

(1)、求证：OB=DC；

(2)、求∠DCO的大小；

(3)、设∠AOB=α，那么当α为多少度时，△COD是等腰三角形．

查看试题解析