广东省惠州市惠东县2021-2022学年八年级上学期期末抽测数学试卷

试卷更新日期：2022-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 中国的方块字中有些也具有对称性，下列美术字是轴对称图形的是（　　）

A、诚 B、信 C、友 D、善

查看试题解析
2. 已知△ABC中，∠A＝20°，∠B＝70°，那么△ABC是（）

A、直角三角形 B、锐角三角形 C、钝角三角形 D、正三角形

查看试题解析
3. 已知△ABC≌△DEF，∠A=80°，∠E=50°，则∠F的度数为（　　）

A、30° B、50° C、80° D、100°

查看试题解析
4. 已知三角形两边长分别为7、11，那么第三边的长可以是（）

A、2 B、3 C、4 D、5

查看试题解析
5. 下列计算正确的是（　　）

A、 $a + 2 a^{2} = 3 a^{3}$ B、 $a^{3} \cdot a^{2} = a^{6}$ C、 ${(a^{3})}^{2} = a^{6}$ D、 ${(- 2 a)}^{2} = - 4 a^{2}$

查看试题解析
6. 若分式 $\frac{1}{x - 2}$ 有意义，则x的取值范围是（）

A、x＝2 B、x＞2 C、x＜2 D、x≠2

查看试题解析
7. 若 $a^{2} + 4 a + k$ 表示一个完全平方式，则k的值为（　　）

A、 $\pm 4$ B、4 C、 $\pm 8$ D、8

查看试题解析
8. 如图，等腰三角形ABC的周长为21，底边BC=5，AB的垂直平分线DE交AB于点D，交AC于点E，则△BEC的周长为（）

A、13 B、14 C、15 D、16

查看试题解析
9. 如图，在△ABC中，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC交AB于M，交AC于N，若BM+CN=9，则线段MN的长为（）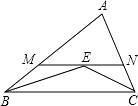

A、6 B、7 C、8 D、9

查看试题解析
10. 如图，△DAC和△EBC均是等边三角形，AE、BD分别与CD、CE交于点M、N，且A、C、B在同一直线上，有如下结论：①△ACE≌△DCB；②CM＝CN；③AC＝DN；④PC平分∠APB；⑤∠APD＝60°，其中正确结论有（）

A、①②③④⑤ B、①②④⑤ C、①②③⑤ D、①②⑤

查看试题解析

二、填空题

11. 分解因式： $x^{2} - 2 x =$ .

查看试题解析
12. 计算： $6 x^{2} y^{3} \div (- 2 x^{2} y) =$

查看试题解析
13. 某种病菌的形状为球形，直径约是 $0.000000102 m$ ，用科学记数法表示这个数为．

查看试题解析
14. 如果多边形的每个内角都等于 $150 °$ ，则它的边数为.

查看试题解析
15. 如图，将一副直角三角板，按如图所示的方式摆放，则∠α的度数是．

查看试题解析
16. 如图，∠DAE＝∠ADE＝15°，AD平分∠BAC，DF⊥AB，若AE＝8，则DF＝．

查看试题解析
17. 如图，在△ABC中，AB＝AC＝10，BC＝12，AD＝8，AD是∠BAC的平分线.若P，Q分别是AD和AC上的动点，则PC+PQ的最小值是.

查看试题解析

三、解答题

18. 计算： $\sqrt{9}$ +|﹣4|+（﹣1）⁰﹣（ $\frac{1}{2}$ ）^﹣¹ ．

查看试题解析
19. 先化简，再求值： $\frac{x}{x^{2} - 1} \div (1 - \frac{1}{x + 1})$ ，其中 $x = \sqrt{3}$ .

查看试题解析
20. 如图， $△ A B C$ 中，EF垂直平分AC，交AC于点F，交BC于点E， $A D ⊥ B C$ ，垂足为D，且 $B D = D E$ ，连接AE．

(1)、求证： $A B = C E$ ；

(2)、若 $△ A B C$ 的周长为14cm， $A C = 6 c m$ ，则DC的长为cm．

查看试题解析
21. 如图，已知CD⊥AB，BE⊥AC，垂足分别为点D，E，且AB＝AC，BE交CD于点O．

(1)、求证：DB＝EC．

(2)、求证：AO平分∠BAC．

查看试题解析
22. 如图，在边长为1的正方形网格中有一个 $△$ ABC，完成下列各图（用无刻度的直尺画图，保留作图痕迹）．
（ 1 ）作 $△$ ABC关于直线MN对称的 $△$ A₁B₁C₁；
（ 2 ）求 $△$ ABC的面积；
（ 3 ）在直线MN上找一点P，使得PA+PB最小．

查看试题解析
23. 某文化用品商店用1000元购进了一批圆规，很快销售一空；商店又用1000元购进了第二批该种圆规，但进价比原来上涨了 $25 %$ ，结果第二次所购进圆规的数量比第一次少40件．

(1)、求两批圆规购进的进价分别是多少；

(2)、若商店将第一批圆规以每件7元，第二批圆规以每件8元的价格全部售出，则共可盈利多少元？

查看试题解析
24. 配方法是数学中非常重要的一种思想方法，它是指将一个式子或一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和的方法．
定义：若一个整数能表示成 $a^{2} + b^{2}$ （a，b是整数）的形式，则称这个数为“完美数”．
例如，5是“完美数”．理由：因为 $5 = 1^{2} + 2^{2}$ ，所以5是“完美数”．

(1)、解决问题：
已知29是“完美数”，请将它写成 $a^{2} + b^{2}$ （a，b是整数）的形式：；

(2)、若 $x^{2} - 4 x + 5$ 可配成 ${(x - m)}^{2} + n$ （m，n为常数），则mn的值为；

(3)、探究问题：
已知 $x^{2} + y^{2} - 2 x + 4 y + 5 = 0$ ，求 $x + y$ 的值．

查看试题解析
25. 在△ABC中，AB＝AC，∠BAC＝100°，点D在BC边上，△ABD和△AFD关于直线AD对称，∠FAC的平分线交BC于点G，连接FG．

(1)、求∠DFG的度数；

(2)、设∠BAD＝θ，
①当θ为何值时，△DFG为等腰三角形；

②△DFG有可能是直角三角形吗？若有，请求出相应的θ值；若没有，请说明理由．

查看试题解析