广东省广州市白云区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 点P（1，﹣2）关于x轴对称的点的坐标为（）

A、（1，2） B、（1，﹣2） C、（﹣1，2） D、（﹣1，﹣2）

查看试题解析
2. 计算：（﹣x³）²＝（）

A、x⁶ B、﹣x⁶ C、x⁵ D、﹣x⁵

查看试题解析
3. 要使分式 $\frac{3 - 5 b}{3 b - 5}$ 有意义，则分式中的字母满足条件（）

A、b＞ $\frac{5}{3}$ B、b≠ $\frac{5}{3}$ C、b＞ $\frac{3}{5}$ D、b≠ $\frac{3}{5}$

查看试题解析
4. 计算：（x＋3）（x﹣2）＝（）

A、x²﹣x﹣6 B、x²＋x﹣6 C、x²﹣6x＋1 D、x²＋6x﹣1

查看试题解析
5. 下列计算中，正确的是（）

A、6a²•3a³＝18a⁵ B、3x²•2x³＝5x⁵ C、2x³•2x³＝4x⁹ D、3y²•2y³＝5y⁶

查看试题解析
6. 下列长度的三条线段，能组成三角形的是（）

A、3，4，8 B、5，6，11 C、5，8，15 D、3，4，6

查看试题解析
7. 方程 $\frac{x}{x - 3} + \frac{1}{3 - x}$ ＝3的解是（）

A、x＝0.5 B、x＝2 C、x＝4 D、x＝5.5

查看试题解析
8. 一个多边形的外角和等于360°，则这个多边形的边数为（）

A、3 B、4 C、5 D、以上均有可能

查看试题解析
9. 计算： $\frac{t^{2} - 2 t + 1}{t^{2} - 4 t + 4} \cdot \frac{t^{2} - 4}{t - 1}$ （）

A、 $\frac{t - 2}{(t - 1) (t + 2)}$ B、 $\frac{t + 2}{(t + 1) (t - 2)}$ C、 $\frac{(t - 1) (t + 2)}{t - 2}$ D、 $\frac{(t + 1) (t - 2)}{t + 2}$

查看试题解析
10. 在△ABC中，AC的垂直平分线DE分别交BC，AC边于点D，E，AE＝3cm，△ABC的周长为13cm，则△ABD的周长为（）cm．

A、5 B、6 C、7 D、8

查看试题解析

二、填空题

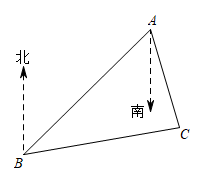
11. 已知△ABC≌△DEF，则BC＝．

查看试题解析
12. 填空： $\frac{6 x^{2}}{3 x^{2} - 3 x y}$ ＝ $\frac{2 x}{()}$ ．

查看试题解析
13. 已知a^m＝2，aⁿ＝3，则a^m-n＝.

查看试题解析
14. 计算：999²＝．

查看试题解析
15. 如图，B处在A处的南偏西45°方向，C处在A处的南偏东15°方向，∠ACB＝85°，则C处在B处的度方向．

查看试题解析
16. 如图，在锐角△ABC中，∠BAC＝60°，AE是中线，两条高BF和CD交于点M，则下列结论中，①BF＝2AF；②∠DMB＝2∠ACD；③AC：AB＝CD：BF；④当点M在AE上时，△ABC是等边三角形．正确的是（填序号）．

查看试题解析

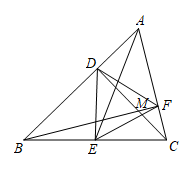
三、解答题

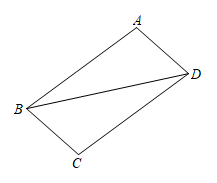
17. 分解因式：36m²﹣4n²

查看试题解析
18. 计算： $\frac{2 a}{a + b} + \frac{2 a b}{a^{2} + a b}$ ．

查看试题解析
19. 如图，在四边形ABCD中，BC∥AD，∠A＝∠C．求证：AB＝CD．

查看试题解析
20. 先化简，再求值：（3x＋2y）²﹣（3x＋y）（3x﹣y），其中x＝ $\frac{1}{3}$ ， y＝﹣1

查看试题解析
21. 如图，把一张长方形的纸ABCD沿EF折叠，重合部分是△MEF．问：△MEF是等腰三角形吗？为什么？

查看试题解析
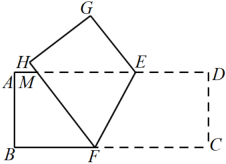22. 如图，在平面直角坐标系xOy中，已知△ABC．

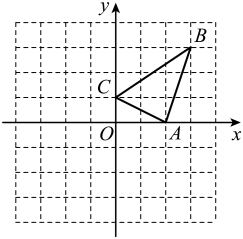(1)、画出与△ABC关于x轴对称的图形；

(2)、在y轴上画出点P，使得AP＋BP最小（保留作图痕迹）．

查看试题解析
23. 如图，在等腰△ABC中，点D在AB边上，点E是AC延长线上的点，DE交底边BC于点G，AE＝3AD＝3BD＝3，

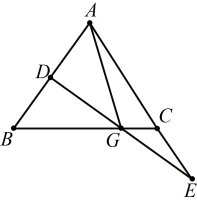(1)、求CE的长度；

(2)、求证：AG是△ADE的中线．

查看试题解析
24. 甲、乙两人同时从A地出发去B地，甲比乙快，甲到达B地后速度变为原来的2倍，并立即返回A地，在距离B地240米处与乙相遇，乙遇到甲后速度也变为原来的2倍，并掉头返回，但甲回到A地时，乙距离A地还有120米，设A，B两地的距离为x米，依题意得：

(1)、两人第一次相遇时，乙所走的路程为米；（用含有x的式子表示）

(2)、甲到达B地前，甲、乙两人的速度比为；（用含有x的式子表示）

(3)、求A，B两地的距离．

查看试题解析
25. 如图，四边形ABDE和四边形ACFG都是正方形，CE与BG交于点M，点M在△ABC的外部．

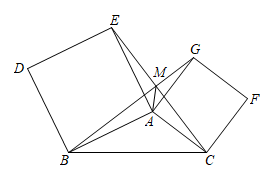(1)、求证：BG＝CE；

(2)、求证：CE⊥BG；

(3)、求：∠AME的度数．

查看试题解析