云南省昭通市昭阳区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-09 类型：期末考试

进入出卷网下载

一、单选题

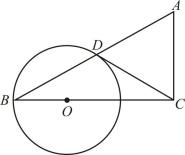
1. 下列事件是必然事件的是（）

A、经过红绿灯路口，遇到绿灯 B、随机买一张电影票，座位号是奇数号 C、没有水分，种子发芽 D、如果a，b都是实数，那么a+b=b+a

查看试题解析
2. 关于x的一元二次方程ax²-2x+1=0有两个相等实数根，则a的值为（）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、1 D、-1

查看试题解析
3. 如图，A，B，C是⊙O上的三点，若∠O=60°，则∠C的度数是（）

A、50° B、40° C、30° D、20°

查看试题解析
4. 疫情期间，某商店连续7天销售口罩的盒数分别为9，11，13，12，11，11，10．关于这组数据，以下结论错误的是（）

A、方差是 $\frac{11}{7}$ B、平均数是11 C、众数是11 D、中位数是11

查看试题解析
5. 在平面直角坐标系中，将二次函数y=x²的图像向右平移3个单位长度，再向上平移1个单位长度所得抛物线对应的函数表达式为（）

A、 $y = (x + 3)^{2} + 1$ B、 $y = (x - 3)^{2} - 1$ C、 $y = (x + 3)^{2} - 1$ D、 $y = (x - 3)^{2} + 1$

查看试题解析
6. 为执行国家药品降价政策，给人民群众带来实惠，某药品经过两次降价，每瓶零售价由200元降为148元，求平均每次降价的百分率．设平均每次降价的百分率为x，可列方程得（）

A、 $148 （ 1 - x ）^{2} = 200$ B、 $200 （ 1 - x ）^{2} = 148$ C、 $148 （ 1 + 2 x ） = 200$ D、 $200 （ 1 + 2 x ） = 148$

查看试题解析
7. 如图，二次函数 $y = a x^{2} + b x + c （ a \neq 0 ）$ 的图像与x轴交于（1，0），及（ $x_{1}$ ， 0）．且﹣2< $x_{1}$ <﹣1，与y轴的交点在（0，2）上方，则下列结论中错误的是（）

A、当 $x \geq - \frac{1}{2}$ 时，y随着x的增大而减少 B、abc>0 C、a+b+c=0 D、关于x的一元二次方程 $a x^{2} + b x + （ c - 2 ） = 0$ 有两个不相等的实数根

查看试题解析
8. 如图，正方形 $A B C D$ 内接于 $⊙ O$ ，线段 $M N$ 在对角线 $B D$ 上运动，若 $⊙ O$ 的面积为 $2 π$ ， $M N = 1$ ，则 $△ A M N$ 周长的最小值是（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题

9. 一元二次方程 $3 x^{2} - 5 x + 7 = 0$ 的二次项系数、一次项系数、常数项的和是．

查看试题解析
10. 二次函数 $y = x^{2} - 2 x - 4$ 的最小值为．

查看试题解析
11. 小明、小辉两家所在位置关于学校中心对称．如果小明家距学校3公里，那么他们两家相距公里．

查看试题解析
12. 一个扇形的弧长是6.3πcm，圆心角是126°，则此扇形的半径是cm．

查看试题解析
13. 小李在双休日到田间参加除草劳动，他随机从锄头、铁锹、镰刀中选用一种劳动工具，则他选到锄头的概率是 .

查看试题解析
14. 如图，正方形ABCD的边长为2，点E是CD的中点，AF平分∠BAE交BC于点F，将△ADE绕点A顺时针旋转90°得△ABG，则CF的长为．

查看试题解析

三、解答题

15. 用适当的方法解下列方程：

(1)、 $（ x - 1 ）^{2} = 4$ ；

(2)、 $x^{2} - 3 x - 4 = 0$ ．

查看试题解析
16. 如图，已知CE=DF，DE=CF．求证：∠CED=∠DFC．

查看试题解析
17. 如图，有一块矩形硬纸板，长20cm，宽10cm．在其四角各剪去一个同样大小的正方形．然后将四周突出部分折起，可制成一个无盖长方体盒子．当剪去正方形的边长取何值时，所得长方体盒子的侧面积为100cm²？

查看试题解析
18. 如图，在平面直角坐标系中，△ABC的顶点坐标分别是A（0，5），B（0，2），C（﹣4，2）．

( 1 )将△ABC以O为旋转中心旋转180°，画出旋转后对应的△A₁B₁C₁；

( 2 )若点A的对应点A₂的坐标为（2，2），画出△ABC平移后得到△A₂B₂C₂ ．

查看试题解析
19. 将背面完全相同，正面上分别写有数字1，2，3，4的四张大小一样的卡片混合后，小明从中随机地抽取一张，把卡片上的数字作为被减数；将形状、大小完全相同，分别标有数字2，3，4的三个小球混合后，小华从中随机地抽取一个，把小球上的数字作为减数，然后计算出这两个数的差．

(1)、请你用画树状图或列表的方法，求这两个数差为0的概率；

(2)、小明与小华做游戏，规则是：若这两个数的差为正数，则小明赢；否则，小华赢．你认为该游戏公平吗？请说明理由．如果不公平，请你修改游戏规则，使游戏公平．

查看试题解析
20. 因疫情防控需要，消毒用品需求量增加．某药店新进一批桶装消毒液，每桶进价45元，每天销售量y（桶）与销售单价x（元）之间满足一次函数关系，当销售单价为50元时，每天的销售量为90桶；当销售单价为60元时，每天的销售量为70桶．

(1)、求y与x之间的函数表达式；

(2)、每桶消毒液的销售价定为多少元时，药店每天获得的利润最大，最大利润是多少元？（利润=销售价－进价）

查看试题解析
21. 如图，在四边形ABCD中，AB=AD，AC⊥BD，垂足为点O，点O是线段AC的中点．

(1)、求证：四边形ABCD是菱形；

(2)、若AD=5，AC=6，求四边形ABCD的面积．

查看试题解析
22. 如图，在△ABC中，∠ACB=90°，点O为BC边上一点，以点O为圆心，OB长为半径的圆与边AB相交于点D，连接DC，且DC=AC．

(1)、求证：DC为⊙O的切线；

(2)、若⊙O的半径为3，CD=4，求BC的长．

查看试题解析
23. 如图，二次函数 $y = a x^{2} - 6 x + c$ 的图像经过点A(﹣1，﹣1)和点B(3，﹣9).

(1)、求该二次函数的表达式.

(2)、求该抛物线的对称轴及顶点坐标.

(3)、点C(m，m)，D都在该函数图象上(其中m>0)，且点C与点D关于抛物线的对称轴对称，求点D的坐标.

查看试题解析