云南省玉溪市峨山彝族自治县2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-10-09 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列说法正确的是( )A、“明天下雨的概率为80%”,意味着明天有80%的时间下雨 B、从两个班级中任选三名学生,至少有两名学生来自同一个班级 C、“某彩票中奖概率是1%”,表示买100张这种彩票一定会有1张中奖 D、小明前几次的数学测试成绩都在90分以上,这次数学测试成绩也一定在90分以上3. 若关于x的一元二次方程的一个根是1,则a的值为( )A、2 B、1 C、0 D、4. 下列各点中,在函数y=- 图象上的是( )A、 B、 C、 D、5. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则sinB的值等于( )
2. 下列说法正确的是( )A、“明天下雨的概率为80%”,意味着明天有80%的时间下雨 B、从两个班级中任选三名学生,至少有两名学生来自同一个班级 C、“某彩票中奖概率是1%”,表示买100张这种彩票一定会有1张中奖 D、小明前几次的数学测试成绩都在90分以上,这次数学测试成绩也一定在90分以上3. 若关于x的一元二次方程的一个根是1,则a的值为( )A、2 B、1 C、0 D、4. 下列各点中,在函数y=- 图象上的是( )A、 B、 C、 D、5. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则sinB的值等于( ) A、 B、 C、 D、6. 如图,点D在△ABC的边AC上,要判断△ADB与△ABC相似,添加一个条件,错误的是( )
A、 B、 C、 D、6. 如图,点D在△ABC的边AC上,要判断△ADB与△ABC相似,添加一个条件,错误的是( ) A、∠ABD=∠C B、∠ADB=∠ABC C、 D、7. 如图,如果从半径为6cm的圆形纸片剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面半径为( )
A、∠ABD=∠C B、∠ADB=∠ABC C、 D、7. 如图,如果从半径为6cm的圆形纸片剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面半径为( )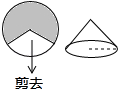 A、2cm B、4cm C、6cm D、8cm8. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中错误的是( )
A、2cm B、4cm C、6cm D、8cm8. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中错误的是( ) A、abc<0 B、b=-4a C、4a+2b≥m(am+b) D、a-b+c>0
A、abc<0 B、b=-4a C、4a+2b≥m(am+b) D、a-b+c>0二、填空题
-
9. 计算:4tan45°= .10. 关于x的一元二次方程 有两个不相等的实数根,则 的取值范围是.
11. 如图,线段AB、CD相交于点E,AC//BD.若AC=3,BD=1.5,BE=2,则AE的长为 . 12. 如图,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是 .
12. 如图,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是 . 13. 如图,已知A为反比例函数y=(x<0)图像上的一点,过点A作AB⊥y轴,垂足为B.若△OAB的面积为1,则k的值为 .
13. 如图,已知A为反比例函数y=(x<0)图像上的一点,过点A作AB⊥y轴,垂足为B.若△OAB的面积为1,则k的值为 . 14. 如图,在△ABC中,∠C=90°,∠B=50°,将△ABC绕点B旋转后,点A落在直线BC上的点A′处,点C落在点C′处,那么∠AA′C′的度数是 .
14. 如图,在△ABC中,∠C=90°,∠B=50°,将△ABC绕点B旋转后,点A落在直线BC上的点A′处,点C落在点C′处,那么∠AA′C′的度数是 .
三、解答题
-
15. 解方程:(1)、;(2)、 .16. 已知反比例函数(为常数,);(1)、若点在这个函数的图象上,求k的值;(2)、若在这个函数图象的每一分支上,y随x的增大而增大,求k的取值范围.17. 如图,在下面的网格图中,每个小正方形的边长均为1个单位长度.在Rt△ABC中,∠C=90°,AC=3,BC=4.

( 1 )试在图中作出△ABC以点A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
( 2 )若点B的坐标为(-3,5),试在图中画出直角坐标系,并根据所画的坐标系作出与△ABC关于原点对称的图形△A2B2C2 , 并写出点C2的坐标.
18. 劳动教育已纳入人才培养全过程,某学校加大投入,建设校园农场,该农场一种作物的产量两年内从300千克增加到363千克.若平均每年的增产率相同,求平均每年的增产率.19. 如图,在和中, , . (1)、求证:;(2)、若 , , 求的长.20. 为庆祝建党100周年,某大学组织志愿者周末到社区进行党史学习宣讲,决定从A , B , C , D四名志愿者中通过抽签的方式确定两名志愿者参加.抽签规则:将四名志愿者的名字分别写在四张完全相同不透明卡片的正面,把四张卡片背面朝上,洗匀后放在桌面上,先从中随机抽取一张卡片,记下名字,再从剩余的三张卡片中随机抽取第二张,记下名字,(1)、“A志愿者被选中”是事件(填“随机”或“不可能”或“必然”);(2)、请你用列表法或画树状图法表示出这次抽签所有可能的结果,并求出A , B两名志愿者被选中的概率.21. 如图,以△PMN的边MN为直径作⊙O,点P在⊙O上,点Q在线段MN的延长线上,PM=PQ,∠Q=30°.
(1)、求证:;(2)、若 , , 求的长.20. 为庆祝建党100周年,某大学组织志愿者周末到社区进行党史学习宣讲,决定从A , B , C , D四名志愿者中通过抽签的方式确定两名志愿者参加.抽签规则:将四名志愿者的名字分别写在四张完全相同不透明卡片的正面,把四张卡片背面朝上,洗匀后放在桌面上,先从中随机抽取一张卡片,记下名字,再从剩余的三张卡片中随机抽取第二张,记下名字,(1)、“A志愿者被选中”是事件(填“随机”或“不可能”或“必然”);(2)、请你用列表法或画树状图法表示出这次抽签所有可能的结果,并求出A , B两名志愿者被选中的概率.21. 如图,以△PMN的边MN为直径作⊙O,点P在⊙O上,点Q在线段MN的延长线上,PM=PQ,∠Q=30°. (1)、求证:直线PQ是⊙O的切线;(2)、若MP= , 求图中阴影部分的面积.22. “互联网+”让我国经济更具活力,直播助销就是运用“互联网+”形成的一种生机勃勃的销售方式.农村电商小李在某电商平台上直播销售一种农产品,每件农产品的成本为40元,每销售一件农产品,需向电商平台缴纳推广费2元.物价部门规定,该农产品的销售单价不高于成本价的2倍,经市场调研发现,每月的销售量y(件)与销售单价x(元)满足如图所示的一次函数关系.
(1)、求证:直线PQ是⊙O的切线;(2)、若MP= , 求图中阴影部分的面积.22. “互联网+”让我国经济更具活力,直播助销就是运用“互联网+”形成的一种生机勃勃的销售方式.农村电商小李在某电商平台上直播销售一种农产品,每件农产品的成本为40元,每销售一件农产品,需向电商平台缴纳推广费2元.物价部门规定,该农产品的销售单价不高于成本价的2倍,经市场调研发现,每月的销售量y(件)与销售单价x(元)满足如图所示的一次函数关系. (1)、求y与x的函数关系式,并写出自变量x的取值范围;(2)、当农产品的销售单价定为多少元时,每月的销售利润最大?最大利润是多少?23. 如图,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C,连接BC,与抛物线的对称轴交于点E,顶点为点D.
(1)、求y与x的函数关系式,并写出自变量x的取值范围;(2)、当农产品的销售单价定为多少元时,每月的销售利润最大?最大利润是多少?23. 如图,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C,连接BC,与抛物线的对称轴交于点E,顶点为点D. (1)、求抛物线的解析式;(2)、若M是抛物线上位于线段BC上方的一个动点,求△BCM的面积的最大值;(3)、点P是对称轴左侧抛物线上的一个动点,点Q在射线ED上,若以点P、Q、E为顶点的三角形与△BOC相似,请直接写出点P的坐标.
(1)、求抛物线的解析式;(2)、若M是抛物线上位于线段BC上方的一个动点,求△BCM的面积的最大值;(3)、点P是对称轴左侧抛物线上的一个动点,点Q在射线ED上,若以点P、Q、E为顶点的三角形与△BOC相似,请直接写出点P的坐标.