云南省普洱市景谷县2021-2022学年九年级上学期期末考试数学试题
试卷更新日期:2022-10-09 类型:期末考试
一、单选题
-
1. 下列有理数 , 其中负数的个数有( ).A、1个 B、2个 C、3个 D、4个2. 如图,若 , ,若 ,则 的度数为( )
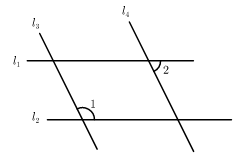 A、 B、 C、 D、3. 如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,该几何体的表面展开图是( )
A、 B、 C、 D、3. 如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,该几何体的表面展开图是( ) A、
A、 B、
B、 C、
C、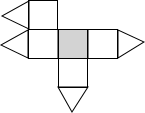 D、
D、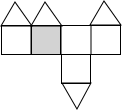 4. 下列运算正确的是( )A、 B、 C、 D、5. 下列方程中,有两个相等实数根的是( )A、 B、 C、 D、6. 下面四个图形中,属于轴对称图形的是( )A、
4. 下列运算正确的是( )A、 B、 C、 D、5. 下列方程中,有两个相等实数根的是( )A、 B、 C、 D、6. 下面四个图形中,属于轴对称图形的是( )A、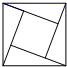 B、
B、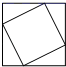 C、
C、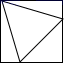 D、
D、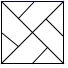 7. 某班对学生的一次数学测试成绩(得分取整数)进行整理后分成五组,并绘制出如图所示的频数直方图,则下列说法中错误的是( )
7. 某班对学生的一次数学测试成绩(得分取整数)进行整理后分成五组,并绘制出如图所示的频数直方图,则下列说法中错误的是( )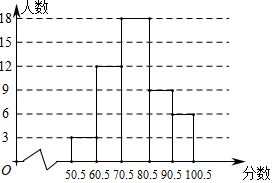 A、有6人的成绩为100分 B、这次共有48人参加测试 C、测试成绩高于70分且不高于80分的人数最多 D、若成绩在80分以上为优秀,则成绩优秀的有15人8. 在平面直角坐标系中,一个智能机器人接到的指令是:从原点O出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点 , 第二次移动到点第n次移动到点 , 则点的坐标是( )
A、有6人的成绩为100分 B、这次共有48人参加测试 C、测试成绩高于70分且不高于80分的人数最多 D、若成绩在80分以上为优秀,则成绩优秀的有15人8. 在平面直角坐标系中,一个智能机器人接到的指令是:从原点O出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点 , 第二次移动到点第n次移动到点 , 则点的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 使 有意义的x的取值范围是 .10. 我国最大的领海是南海,总面积有3500000km2,用科学记数法可以表示为 km2.11. 函数y=kx与y=6﹣x的图象如图所示,则不等式6﹣x≥kx的解集为 .
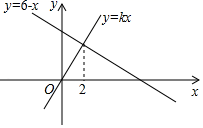 12. 若 , 则 .13. 如图,在平行四边形 中,点M为边 上一点, ,点E,点 分别是 中点,若 ,则 的长为.
12. 若 , 则 .13. 如图,在平行四边形 中,点M为边 上一点, ,点E,点 分别是 中点,若 ,则 的长为.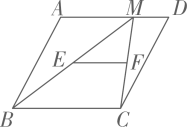 14. 如图,是的外接圆, , 则弦 .
14. 如图,是的外接圆, , 则弦 .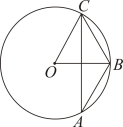
三、解答题
-
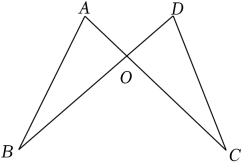
15. 先化简,再求值:( ) ,其中x= +1.16. 已知:如图,OA=OD,OB=OC.求证:∠B=∠C.
 17. 某校组织全校1800名学生参加建党“百年华诞”诗词诵读活动,并在活动之后举办诗词大赛.为了解本次活动的持续效果,团委在活动启动初期,随机抽取50名学生调查“一周诗词背诵数量”,绘得统计表.大赛结束后一个月,再次抽查这部分学生“一周诗词背诵数量”,绘得统计图.请根据调查的信息,解答下列问题:
17. 某校组织全校1800名学生参加建党“百年华诞”诗词诵读活动,并在活动之后举办诗词大赛.为了解本次活动的持续效果,团委在活动启动初期,随机抽取50名学生调查“一周诗词背诵数量”,绘得统计表.大赛结束后一个月,再次抽查这部分学生“一周诗词背诵数量”,绘得统计图.请根据调查的信息,解答下列问题:一周诗词背诵数量统计表
一周诗词诵背数量
3首
4首
5首
6首
7首
8首
人数
8
7
13
10
8
4
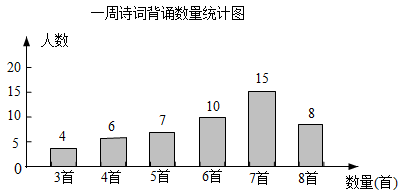 (1)、求活动初期被抽查的学生“一周诗词背诵数量”的中位数;(2)、估计大赛后一个月,该校学生一周诗词背诵6首(含6首)以上的人数.18. 防疫期间,全市所有学校都严格落实测体温进校园的防控要求.某校开设了A、B、C三个测温通道,某天早晨,该校小明和小丽两位同学将随机通过测温通道进入校园.(1)、小明从A测温通道通过的概率是;(2)、利用画树状图或列表的方法,求小明和小丽从同一个测温通道通过的概率.19. 如图,将矩形沿对角线对折,点B的对应点为 , 交于E点.交于F.
(1)、求活动初期被抽查的学生“一周诗词背诵数量”的中位数;(2)、估计大赛后一个月,该校学生一周诗词背诵6首(含6首)以上的人数.18. 防疫期间,全市所有学校都严格落实测体温进校园的防控要求.某校开设了A、B、C三个测温通道,某天早晨,该校小明和小丽两位同学将随机通过测温通道进入校园.(1)、小明从A测温通道通过的概率是;(2)、利用画树状图或列表的方法,求小明和小丽从同一个测温通道通过的概率.19. 如图,将矩形沿对角线对折,点B的对应点为 , 交于E点.交于F. (1)、求证:四边形是菱形;(2)、若 , , 求的长.20. 学校需要购买一些篮球和足球,已知篮球的单价比足球的单价贵30元,买2个篮球和3个足球一共需要510元.(1)、求篮球和足球的单价;(2)、根据学生体育活动的需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的 , 学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?21. 如图,大、小两个正方形的中心均与平面直角坐标系的原点O重合,边分别与坐标轴平行,反比例函数 的图象与大正方形的一边交于点A(1,2),且经过小正方形的顶点B.
(1)、求证:四边形是菱形;(2)、若 , , 求的长.20. 学校需要购买一些篮球和足球,已知篮球的单价比足球的单价贵30元,买2个篮球和3个足球一共需要510元.(1)、求篮球和足球的单价;(2)、根据学生体育活动的需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的 , 学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?21. 如图,大、小两个正方形的中心均与平面直角坐标系的原点O重合,边分别与坐标轴平行,反比例函数 的图象与大正方形的一边交于点A(1,2),且经过小正方形的顶点B. (1)、求反比例函数的解析式;(2)、求图中阴影部分的面积.
(1)、求反比例函数的解析式;(2)、求图中阴影部分的面积.