云南省红河哈尼族彝族自治州建水县2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-10-09 类型:期末考试
一、单选题
-
1. 观察下列四个图形,中心对称图形是( )A、
 B、
B、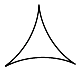 C、
C、 D、
D、 2. 下列事件中,是必然事件的是( )A、购买1张彩票,中奖 B、任意画一个三角形,其内角和是180° C、随意翻到一本书的某页,这页的页码是奇数 D、射击运动员射击一次,命中靶心3. 若方程 是关于x的一元二次方程,则( )A、 B、m=2 C、m=-2 D、4. 用一个圆心角为 , 半径为6的扇形做一个圆锥的侧面,则这个圆锥的底面圆的面积为( ).A、 B、 C、 D、5. 某商品原售价是200元,经过连续两次降价后售价为162元,设平均每次降百分率为x,则下面所列方程中正确的是( )A、 B、 C、 D、6. 在平面直角坐标系中,对于二次函数 , 下列说法中错误的是( )A、y的最小值为1 B、图象顶点坐标为(2,1),对称轴为直线x=2 C、当时,y的值随x值的增大而增大,当时,y的值随x值的增大而减小 D、它的图象可由的图象向右平移2个单位长度,再向上平移1个单位长度得到7. 如图,AB是⊙O的直径,C,D两点在⊙O上,若∠ABD=50°,则∠C的度数为( )
2. 下列事件中,是必然事件的是( )A、购买1张彩票,中奖 B、任意画一个三角形,其内角和是180° C、随意翻到一本书的某页,这页的页码是奇数 D、射击运动员射击一次,命中靶心3. 若方程 是关于x的一元二次方程,则( )A、 B、m=2 C、m=-2 D、4. 用一个圆心角为 , 半径为6的扇形做一个圆锥的侧面,则这个圆锥的底面圆的面积为( ).A、 B、 C、 D、5. 某商品原售价是200元,经过连续两次降价后售价为162元,设平均每次降百分率为x,则下面所列方程中正确的是( )A、 B、 C、 D、6. 在平面直角坐标系中,对于二次函数 , 下列说法中错误的是( )A、y的最小值为1 B、图象顶点坐标为(2,1),对称轴为直线x=2 C、当时,y的值随x值的增大而增大,当时,y的值随x值的增大而减小 D、它的图象可由的图象向右平移2个单位长度,再向上平移1个单位长度得到7. 如图,AB是⊙O的直径,C,D两点在⊙O上,若∠ABD=50°,则∠C的度数为( )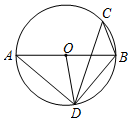 A、25° B、30° C、40° D、50°8. 二次函数y=ax2+bx+c(a≠0)图象如图所示,现有下列结论:①b2﹣4ac>0;②a>0;③b>0;④c>0;⑤4a+2b+c<0,则其中结论正确的个数是( )
A、25° B、30° C、40° D、50°8. 二次函数y=ax2+bx+c(a≠0)图象如图所示,现有下列结论:①b2﹣4ac>0;②a>0;③b>0;④c>0;⑤4a+2b+c<0,则其中结论正确的个数是( )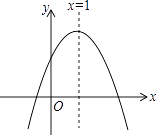 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
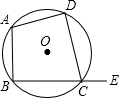
9. 已知3是关于x的方程x2﹣2x﹣n=0的一个根,则n的值为.10. 若二次函数 的图象与 轴有交点,则 的取值范围是 .11. 已知点与关于原点对称,则 .12. 如图,四边形ABCD为⊙O的内接四边形,∠A=100°,则∠DCE的度数为;
 13. 一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有9个黄球 每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在 ,那么估计盒子中小球的个数是.14. 等腰三角形 中,顶角 为 ,点 在以 为圆心, 长为半径的圆上,且 ,则 的度数为 .
13. 一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有9个黄球 每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在 ,那么估计盒子中小球的个数是.14. 等腰三角形 中,顶角 为 ,点 在以 为圆心, 长为半径的圆上,且 ,则 的度数为 .三、解答题
-
15. 解方程:(1)、(2)、16. 如图,已知三个顶点的坐标分别为 , 在给出的平面直角坐标系中:
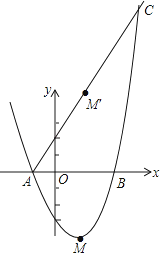
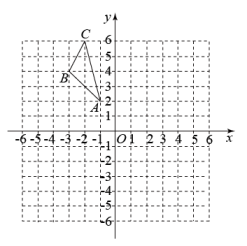 (1)、面出绕点A顺时针旋转后得到的;并直接写出的坐标;(2)、计算点B旋转到点位置时,经过的路径长.17. 在校运动会上,小华在某次试投中,铅球所经过的路线是如图所示的抛物线的一部分,如图所示建立平面直角坐标系.已知铅球出手处A距离地面的高度是米,当铅球运行的水平距离为4米时,达到最大高度3米的B处.小华此次投掷的成绩是多少米?
(1)、面出绕点A顺时针旋转后得到的;并直接写出的坐标;(2)、计算点B旋转到点位置时,经过的路径长.17. 在校运动会上,小华在某次试投中,铅球所经过的路线是如图所示的抛物线的一部分,如图所示建立平面直角坐标系.已知铅球出手处A距离地面的高度是米,当铅球运行的水平距离为4米时,达到最大高度3米的B处.小华此次投掷的成绩是多少米?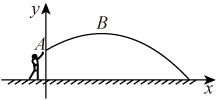 18. 校生物小组有一块长32m,宽20m的矩形实验田,为了管理方便,准备沿平行于两边的方向纵、横个开辟一条等宽的小道,要使种植面积为540m2 , 小道的宽应是多少米?
18. 校生物小组有一块长32m,宽20m的矩形实验田,为了管理方便,准备沿平行于两边的方向纵、横个开辟一条等宽的小道,要使种植面积为540m2 , 小道的宽应是多少米?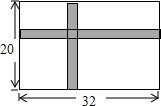 19. 为庆祝中国共产党成立100周年,某市组织该市七、八两个年级学生参加演讲比赛,演讲比赛的主题为“追忆百年历程,凝聚青春力量”该市一中学经过初选,在七年级选出3名同学,其中2名女生,分别记 、 ,1名男生,记为 ;在八年级选出3名同学,其中1名女生,记为 ,2名男生,分别记为 、 .现分别从两个年级初选出的同学中,每个年级随机选出一名同学组成代表队参加比赛.(1)、用列表法或树状图法(树状图也称树形图)中的一种方法,求所有可能出现的代表队总数;(2)、求选出的代表队中的两名同学恰好是一名男生和一名女生的概率P .20. 如图,在⊙O中,DE是⊙O的直径,AB是⊙O的弦,AB的中点C在直径DE上.已知AB=8cm,CD=2cm
19. 为庆祝中国共产党成立100周年,某市组织该市七、八两个年级学生参加演讲比赛,演讲比赛的主题为“追忆百年历程,凝聚青春力量”该市一中学经过初选,在七年级选出3名同学,其中2名女生,分别记 、 ,1名男生,记为 ;在八年级选出3名同学,其中1名女生,记为 ,2名男生,分别记为 、 .现分别从两个年级初选出的同学中,每个年级随机选出一名同学组成代表队参加比赛.(1)、用列表法或树状图法(树状图也称树形图)中的一种方法,求所有可能出现的代表队总数;(2)、求选出的代表队中的两名同学恰好是一名男生和一名女生的概率P .20. 如图,在⊙O中,DE是⊙O的直径,AB是⊙O的弦,AB的中点C在直径DE上.已知AB=8cm,CD=2cm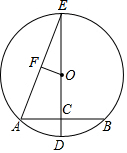 (1)、求⊙O的面积;(2)、连接AE,过圆心O向AE作垂线,垂足为F,求OF的长.21. 为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80,设这种产品每天的销售利润为w元.(1)、求w与x之间的函数关系式.(2)、该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(1)、求⊙O的面积;(2)、连接AE,过圆心O向AE作垂线,垂足为F,求OF的长.21. 为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80,设这种产品每天的销售利润为w元.(1)、求w与x之间的函数关系式.(2)、该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?