安徽省宣城市2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-10-09 类型:期末考试
一、单选题
-
1. 已知点A(1,y1),B(2,y2)在抛物线y=(x+1)2+2上,则下列结论正确的是( ).A、 B、 C、 D、2. 下列各组的四条线段 , , , 是成比例线段的是( )A、 , , , B、 , , , C、 , , , D、 , , ,3. 函数y=的图象中,在每个象限内y随x增大而增大,则k可能为( )A、﹣2 B、﹣1 C、0 D、14. 如图,某停车场入口的栏杆AB,从水平位置绕点O旋转到A′B′的位置,已知AO的长为4米.若栏杆的旋转角∠AOA′=α,则栏杆A端升高的高度为( )
 A、 米 B、4sinα米 C、 米 D、4cosα米5. 以下有关抛物线的结论,正确的是( ).A、开口向上 B、与y轴的交点坐标是 C、与x轴只有一个交点 D、顶点坐标是6. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
A、 米 B、4sinα米 C、 米 D、4cosα米5. 以下有关抛物线的结论,正确的是( ).A、开口向上 B、与y轴的交点坐标是 C、与x轴只有一个交点 D、顶点坐标是6. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )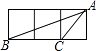 A、
A、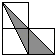 B、
B、 C、
C、 D、
D、 7. △ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列四个选项中,错误的是( )
7. △ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列四个选项中,错误的是( ) A、sinα=cosα B、tanC=2 C、sinβ=cosβ D、tanα=18. 共享单车为市民出行带来了方便,某单车公司第一个月投放a辆单车,计划第三个月投放单车y辆,设该公司第二、三两个月投放单车数量的月平均增长率为x,那么y与x的函数关系是( )A、y=x2+a B、y=a(1+x)2 C、y=(1﹣x)2+a D、y=a(1﹣x)29. 如图,乐器上的一根弦AB=80cm , 两个端点A , B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,则C , D之间的距离为( )
A、sinα=cosα B、tanC=2 C、sinβ=cosβ D、tanα=18. 共享单车为市民出行带来了方便,某单车公司第一个月投放a辆单车,计划第三个月投放单车y辆,设该公司第二、三两个月投放单车数量的月平均增长率为x,那么y与x的函数关系是( )A、y=x2+a B、y=a(1+x)2 C、y=(1﹣x)2+a D、y=a(1﹣x)29. 如图,乐器上的一根弦AB=80cm , 两个端点A , B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,则C , D之间的距离为( ) A、(40 ﹣40)cm B、(80 ﹣40)cm C、(120﹣40 )cm D、(80 ﹣160)cm10. 正方形ABCD中,AB=4,P为对角线BD上一动点,F为射线AD上一点,若AP=PF,则△APF的面积最大值为( )
A、(40 ﹣40)cm B、(80 ﹣40)cm C、(120﹣40 )cm D、(80 ﹣160)cm10. 正方形ABCD中,AB=4,P为对角线BD上一动点,F为射线AD上一点,若AP=PF,则△APF的面积最大值为( ) A、8 B、6 C、4 D、
A、8 B、6 C、4 D、二、填空题
-
11. 若 , 且 , 则 .12. 如图,某水库大坝的横断面是梯形,坝外斜坡的坡比 , 两个坡角的和为75°,则坝内斜坡的坡比是 .
 13. 如图,在平面直角坐标系中,ABCO为平行四边形,O(0,0),A(3,1),B(1,2),反比例函数 的图象经过▱OABC的顶点C,则k= .
13. 如图,在平面直角坐标系中,ABCO为平行四边形,O(0,0),A(3,1),B(1,2),反比例函数 的图象经过▱OABC的顶点C,则k= . 14. 如图,正方形ABCD中,点F在边AB上,且AF:FB=1:2,AC与DF交于点N .
14. 如图,正方形ABCD中,点F在边AB上,且AF:FB=1:2,AC与DF交于点N .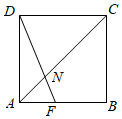 (1)、当AB=4时,AN= .(2)、S△ANF:S四边形CNFB= . (S表示面积)
(1)、当AB=4时,AN= .(2)、S△ANF:S四边形CNFB= . (S表示面积)三、解答题
-
15. 计算:tan45°+4cos30°sin45° tan60°.16. 已知线段a,b,c满足 , 且 . 求线段a,b,c的长.17. 如图,一次函数y1=kx+b的图象与反比性函数y2= 的图象交于A(2,1)、B(-1,n)两点.
 (1)、利用图中的条件,求反比例函数和一次函数的解析式;(2)、根据图象直接写出使y1 y2的自变量x取值范围.18. 如图,在的网格图中,每个小正方形边长均为1,原点O和的顶点均为格点.
(1)、利用图中的条件,求反比例函数和一次函数的解析式;(2)、根据图象直接写出使y1 y2的自变量x取值范围.18. 如图,在的网格图中,每个小正方形边长均为1,原点O和的顶点均为格点. (1)、以O为位似中心,在网格图中作 , 使与位似,且位似比为;(2)、写出点、点、点的坐标.19. 已知:如图,在 中, , 于 , 为直角边 的中点,射线 交 的延长线于点 .
(1)、以O为位似中心,在网格图中作 , 使与位似,且位似比为;(2)、写出点、点、点的坐标.19. 已知:如图,在 中, , 于 , 为直角边 的中点,射线 交 的延长线于点 . (1)、若 , ,求 长;(2)、求证: .20. 2022年北京冬奥会即将召开,激起了人们对冰雪运动的极大热情,如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系,图中的抛物线C1:y=﹣x2+x+1近似表示滑雪场地上的一座小山坡,某运动员从点O正上方4米处的A点滑出,滑出后沿一段抛物线C2:y=﹣x2+bx+c运动.
(1)、若 , ,求 长;(2)、求证: .20. 2022年北京冬奥会即将召开,激起了人们对冰雪运动的极大热情,如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系,图中的抛物线C1:y=﹣x2+x+1近似表示滑雪场地上的一座小山坡,某运动员从点O正上方4米处的A点滑出,滑出后沿一段抛物线C2:y=﹣x2+bx+c运动.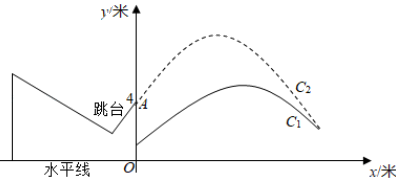 (1)、当运动员运动到离A处的水平距离为4米时,离水平线的高度为8米,求抛物线C2的函数解析式(不要求写出自变量x的取值范围);(2)、在(1)的条件下,当运动员运动的水平距离为多少米时,运动员与小山坡的竖直距离为1米?21. 如图1,为放置在水平桌面上的台灯,底座的高为.长度均为的连杆 , 与始终在同一水平面上.
(1)、当运动员运动到离A处的水平距离为4米时,离水平线的高度为8米,求抛物线C2的函数解析式(不要求写出自变量x的取值范围);(2)、在(1)的条件下,当运动员运动的水平距离为多少米时,运动员与小山坡的竖直距离为1米?21. 如图1,为放置在水平桌面上的台灯,底座的高为.长度均为的连杆 , 与始终在同一水平面上. (1)、旋转连杆 , , 使成平角, , 如图2,求连杆端点D离桌面l的高度.(2)、将(1)中的连杆绕点C逆时针旋转,使 , 如图3,问此时连杆端点D离桌面l的高度是增加了还是减少?增加或减少了多少?(精确到 , 参考数据: , )22. 2022年冬奥会即将在北京召开,某网络经销商购进了一批以冬奥会为主题的文化衫进行销售,文化衫的进价为每件30元,当销售单价定为70元时,每天可售出20件,每销售一件需缴纳网络平台管理费2元,为了扩大销售,增加盈利,决定采取适当的降价措施,经调查发现:销售单价每降低1元,则每天可多售出2件(销售单价不低于进价),若设这款文化衫的销售单价为x(元),每天的销售量为y(件).(1)、求每天的销售量y(件)与销售单价x(元)之间的函数关系式;(2)、当销售单价为多少元时,销售这款文化衫每天所获得的利润最大,最大利润为多少元?23. 如图1,在四边形ABCD中, , 点E在边BC上,且 , , 作交线段AE于点F,连接BF.
(1)、旋转连杆 , , 使成平角, , 如图2,求连杆端点D离桌面l的高度.(2)、将(1)中的连杆绕点C逆时针旋转,使 , 如图3,问此时连杆端点D离桌面l的高度是增加了还是减少?增加或减少了多少?(精确到 , 参考数据: , )22. 2022年冬奥会即将在北京召开,某网络经销商购进了一批以冬奥会为主题的文化衫进行销售,文化衫的进价为每件30元,当销售单价定为70元时,每天可售出20件,每销售一件需缴纳网络平台管理费2元,为了扩大销售,增加盈利,决定采取适当的降价措施,经调查发现:销售单价每降低1元,则每天可多售出2件(销售单价不低于进价),若设这款文化衫的销售单价为x(元),每天的销售量为y(件).(1)、求每天的销售量y(件)与销售单价x(元)之间的函数关系式;(2)、当销售单价为多少元时,销售这款文化衫每天所获得的利润最大,最大利润为多少元?23. 如图1,在四边形ABCD中, , 点E在边BC上,且 , , 作交线段AE于点F,连接BF. (1)、求证:(2)、如图2,若 , , , 求BE的长;(3)、如图3,若BF的延长线经过AD的中点M,求的值.
(1)、求证:(2)、如图2,若 , , , 求BE的长;(3)、如图3,若BF的延长线经过AD的中点M,求的值.