安徽省宿州市埇桥区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-10-09 类型:期末考试
一、单选题
-
1. 已知a,b,c,d是成比例线段,其中 , , ,则线段d的长度是( )A、 B、 C、 D、2. 在平面直角坐标系 中,对于横、纵坐标相等的点称为“好点”.下列函数的图象中不存在“好点”的是( )A、 B、 C、 D、3. 如图,在平面直角坐标中,点P的坐标为(3,4),则射线OP与x轴正方向所夹锐角a的余弦值为( )
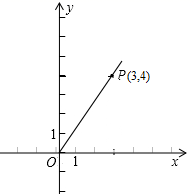 A、 B、 C、 D、4. 正方形ABCD的对角线相交于点O,正方形与正方形ABCD的边长相等.在正方形绕点O旋转的过程中,两个正方形重叠部分的面积是2,则AD的长为( )
A、 B、 C、 D、4. 正方形ABCD的对角线相交于点O,正方形与正方形ABCD的边长相等.在正方形绕点O旋转的过程中,两个正方形重叠部分的面积是2,则AD的长为( )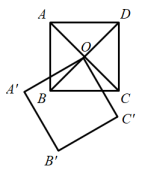 A、1 B、 C、2 D、5. 图2是图1中长方体的三视图,若用S表示面积, , ,则 ( )
A、1 B、 C、2 D、5. 图2是图1中长方体的三视图,若用S表示面积, , ,则 ( )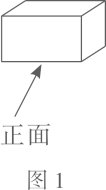
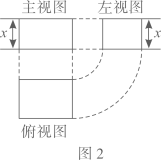 A、 B、 C、 D、6. 已知是关于x的一元二次方程的一个根,则该方程的另一个根为( )A、 B、 C、 D、7. 已知四边形 是平行四边形, , 相交于点O,下列结论错误的是( )A、 , B、当 时,四边形 是菱形 C、当 时,四边形 是矩形 D、当 且 时,四边形 是正方形8. 关于反比例函数 的图象,下列说法中, 错误的是( )A、点(1,-1)在它的图象上 B、图象位于第二 、四象限 C、图象的两个分支关于原点对称 D、x的值越大,图象越接近x轴9. 二次函数 的图象如图所示,下列结论:① ;② ;③ ;④当 时,y随x的增大而减小,其中正确的有( )
A、 B、 C、 D、6. 已知是关于x的一元二次方程的一个根,则该方程的另一个根为( )A、 B、 C、 D、7. 已知四边形 是平行四边形, , 相交于点O,下列结论错误的是( )A、 , B、当 时,四边形 是菱形 C、当 时,四边形 是矩形 D、当 且 时,四边形 是正方形8. 关于反比例函数 的图象,下列说法中, 错误的是( )A、点(1,-1)在它的图象上 B、图象位于第二 、四象限 C、图象的两个分支关于原点对称 D、x的值越大,图象越接近x轴9. 二次函数 的图象如图所示,下列结论:① ;② ;③ ;④当 时,y随x的增大而减小,其中正确的有( )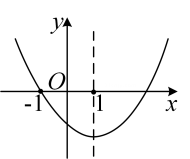 A、4个 B、3个 C、2个 D、1个10. 如图,在△ABC与△ADE中,∠ACB =∠AED =90°,∠ABC=∠ADE , 连接BD、CE , 若AC︰BC=3︰4,则BD︰CE为( )
A、4个 B、3个 C、2个 D、1个10. 如图,在△ABC与△ADE中,∠ACB =∠AED =90°,∠ABC=∠ADE , 连接BD、CE , 若AC︰BC=3︰4,则BD︰CE为( )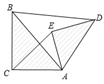 A、5︰3 B、4︰3 C、 ︰2 D、2︰
A、5︰3 B、4︰3 C、 ︰2 D、2︰二、填空题
-
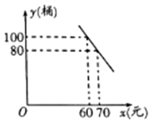
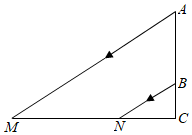
11. 已知: , 则锐角的度数为 .12. 若关于x的一元二次方程 有实数根,则n的取值范围是.13. 如图,AB表示一个窗户的高,AM和BN表示射入室内的光线,窗户的下端到地面的距离BC=1m.已知某一时刻BC在地面的影长CN=1.5m,AC在地面的影长CM=4.5m,则窗户的高度为m.
 14. 如图,将矩形纸片沿过点C的直线折叠,使得点B落在矩形内点处,折痕为 .
14. 如图,将矩形纸片沿过点C的直线折叠,使得点B落在矩形内点处,折痕为 . (1)、点恰好为中点时,的值为 .(2)、点在上且D、、E在同一条直线上时,的值为 .
(1)、点恰好为中点时,的值为 .(2)、点在上且D、、E在同一条直线上时,的值为 .三、解答题
-
15. 计算:16. 反比例函数的图象经过点A(2,3).(1)、求这个函数的解析式;(2)、请判断点B(1,6)是否在这个反比例函数的图象上,并说明理由.17. 已知,平面直角坐标系中,的位置如图所示,点A、B、C的坐标分别为、、 . 与是以点P为位似中心的位似图形;
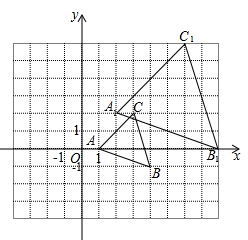 (1)、请画出点P的位置,井写出点P的坐标;(2)、请以点O为位似中心在y轴左侧,画出的位似图形 , 使相似比为 , 若点为内一点,则点M在内的对应点的坐标为 .18. 小颖和小亮都想去观看“垃圾分类”宣传演出,但只有一张入场券,于是他们设计了一个“配紫色”游戏:A,B是两个可以自由转动的转盘,每个转盘都被分成面积相等的几个扇形、同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么可以配成紫色.若配成紫色,则小颖去观看,否则小亮去观看.这个游戏对双方公平吗?请说明理由.
(1)、请画出点P的位置,井写出点P的坐标;(2)、请以点O为位似中心在y轴左侧,画出的位似图形 , 使相似比为 , 若点为内一点,则点M在内的对应点的坐标为 .18. 小颖和小亮都想去观看“垃圾分类”宣传演出,但只有一张入场券,于是他们设计了一个“配紫色”游戏:A,B是两个可以自由转动的转盘,每个转盘都被分成面积相等的几个扇形、同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么可以配成紫色.若配成紫色,则小颖去观看,否则小亮去观看.这个游戏对双方公平吗?请说明理由.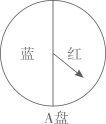
 19. 已知,为的中线,是的中线, .
19. 已知,为的中线,是的中线, .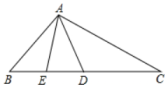 (1)、判断与是否相似,并说明理由;(2)、求证: .20. 某无人机兴趣小组在操场上开展活动(如图),此时无人机在离地面30米的D处,无人机测得操控者A的俯角为37°,测得点C处的俯角为45°.又经过人工测量操控者A和教学楼BC距离为57米,求教学楼BC的高度.(注:点A,B,C,D都在同一平面上.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(1)、判断与是否相似,并说明理由;(2)、求证: .20. 某无人机兴趣小组在操场上开展活动(如图),此时无人机在离地面30米的D处,无人机测得操控者A的俯角为37°,测得点C处的俯角为45°.又经过人工测量操控者A和教学楼BC距离为57米,求教学楼BC的高度.(注:点A,B,C,D都在同一平面上.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)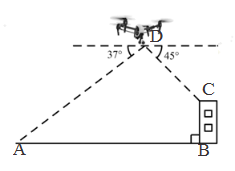
21. 二次函数的图象与y轴交于点.(1)、求出m的值,并求它与x轴的交点和抛物线顶点的坐标;(2)、x取什么值时,抛物线在x轴上方?(3)、将该抛物线先向右平移1个单位,再向下平移2个单位,请直接写出所得新抛物线的表达式.