安徽省宿州市萧县2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-10-09 类型:期末考试
一、单选题
-
1. 矩形,菱形,正方形不同时具有的性质是( )A、对边平行且相等 B、对角相等 C、对角线互相平分 D、每条对角线平分一组对角2. 方程(x-2)(x-4)=0 的两个根是等腰三角形的底和腰,则这个等腰三角形的周长为 ( )A、6 B、8 C、10 D、8或103. 下列各组线段中,成比例的是( )A、2cm,3cm,4cm,5cm B、2cm,4cm,6cm,8cm C、3cm,6cm,8cm,12cm D、1cm,3cm,5cm,15cm4. 下列几何体是由4个相同的小正方体搭成的,其中从正面和上面看到的平面图形相同的是( )A、
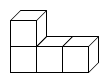 B、
B、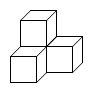 C、
C、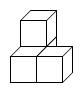 D、
D、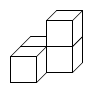 5. 如果反比例函数的图象经过点 , 则k=( )A、18 B、 C、16 D、6. 如图,在菱形 中, 于点 , , ,则菱形的边长为( ).
5. 如果反比例函数的图象经过点 , 则k=( )A、18 B、 C、16 D、6. 如图,在菱形 中, 于点 , , ,则菱形的边长为( ).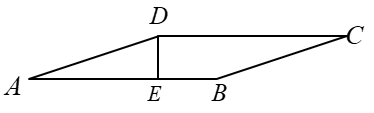 A、 B、 C、5 D、7. 从﹣1,0,1三个数中任取两个不同的数作为点的坐标,则该点在坐标轴上的概率为( )A、 B、 C、 D、8. 慧慧将方程2x2+4x﹣7=0通过配方转化为(x+n)2=p的形式,则p的值为( )A、7 B、8 C、3.5 D、4.59. 如图,Rt△OAB中,∠OAB=90°,点A在x轴上,反比例函数y=(x>0)的图象过斜边OB的中点D,与AB交于点C.若△OBC的面积为3,则k的值是( )
A、 B、 C、5 D、7. 从﹣1,0,1三个数中任取两个不同的数作为点的坐标,则该点在坐标轴上的概率为( )A、 B、 C、 D、8. 慧慧将方程2x2+4x﹣7=0通过配方转化为(x+n)2=p的形式,则p的值为( )A、7 B、8 C、3.5 D、4.59. 如图,Rt△OAB中,∠OAB=90°,点A在x轴上,反比例函数y=(x>0)的图象过斜边OB的中点D,与AB交于点C.若△OBC的面积为3,则k的值是( )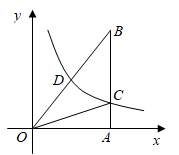 A、 B、 C、 D、10. 如图, , 已知 , , 则的值为( )
A、 B、 C、 D、10. 如图, , 已知 , , 则的值为( )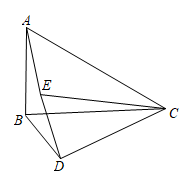 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若方程(m+1)x|m|+1﹣2x=5是关于x的一元二次方程,则m的值为 .12. 有一些乒乓球,不知其数,先取12个做了标记,把它们放回袋中,混合均匀后又取了20个,发现含有2个做标记,可估计袋中乒乓球有个 .13. 某矩形的长为a,宽为b,且(a+b)(a+b+2)=8,则a+b的值为 .14. 如图,正方形ABCD中,点F在边AB上,且AF:FB=1:2,AC与DF交于点N .
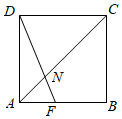 (1)、当AB=4时,AN= .(2)、S△ANF:S四边形CNFB= . (S表示面积)
(1)、当AB=4时,AN= .(2)、S△ANF:S四边形CNFB= . (S表示面积)三、解答题
-
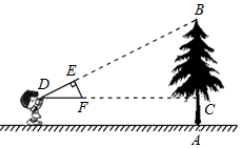
15. 解方程:16. 如图,小亮同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与树顶B在同一直线上.已知纸板的两条边EF=30cm,DE=40cm,延长DF交AB于点C,测得边DF离地面的高度AC=1.5m,CD=12m,求树高AB.
 17. 如图,在平行四边形ABCD中,点O是AB的中点,且OC=OD.
17. 如图,在平行四边形ABCD中,点O是AB的中点,且OC=OD. (1)、求证:平行四边形ABCD是矩形;(2)、若AD=3,∠COD=60°,求矩形ABCD的面积.18. 某中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米.设这个苗圃园垂直于墙的一边的长为x米
(1)、求证:平行四边形ABCD是矩形;(2)、若AD=3,∠COD=60°,求矩形ABCD的面积.18. 某中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米.设这个苗圃园垂直于墙的一边的长为x米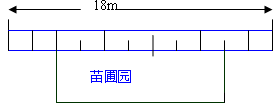 (1)、用含x的代数式表示平行于墙的一边的长为米,.x的取值范围为(2)、这个苗圃园的面积为88平方米时,求x的值19. 如图,在由边长为1个单位长度的小正方形组成的网格中,已知点O,A,B,C均为网格线的交点.
(1)、用含x的代数式表示平行于墙的一边的长为米,.x的取值范围为(2)、这个苗圃园的面积为88平方米时,求x的值19. 如图,在由边长为1个单位长度的小正方形组成的网格中,已知点O,A,B,C均为网格线的交点.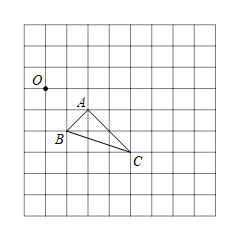 (1)、以O为位似中心,在网格中画出的位似图形 , 使原图形与新图形的位似比为;(2)、把向上平移3个单位长度得 , 请画出;(3)、若的面积为S,用S表示出的面积,直接写出结果.20. 为了响应国家有关开展中小学生“课后服务”的政策,某学校课后开设了A:课后作业辅导、B:书法、C:阅读、D:绘画、E:器乐,五门课程供学生选择;其中A(必选项目),再从B、C、D、E中选两门课程.(1)、若学生小玲第一次选一门课程,直接写出学生小玲选中项目E的概率;(2)、若学生小强和小明在选项的过程中,第一次都是选了项目E , 那么他俩第二次同时选择书法或绘画的概率是多少?请用列表法或画树状图的方法加以说明并列出所有等可能的结果.21. 在四边形ABCD中, . 点E在AB上,过点E作交CD于点F.
(1)、以O为位似中心,在网格中画出的位似图形 , 使原图形与新图形的位似比为;(2)、把向上平移3个单位长度得 , 请画出;(3)、若的面积为S,用S表示出的面积,直接写出结果.20. 为了响应国家有关开展中小学生“课后服务”的政策,某学校课后开设了A:课后作业辅导、B:书法、C:阅读、D:绘画、E:器乐,五门课程供学生选择;其中A(必选项目),再从B、C、D、E中选两门课程.(1)、若学生小玲第一次选一门课程,直接写出学生小玲选中项目E的概率;(2)、若学生小强和小明在选项的过程中,第一次都是选了项目E , 那么他俩第二次同时选择书法或绘画的概率是多少?请用列表法或画树状图的方法加以说明并列出所有等可能的结果.21. 在四边形ABCD中, . 点E在AB上,过点E作交CD于点F. (1)、若 , 如图1,则EF的长;(2)、若 , 如图2,则EF的长;(3)、若 , 如图3,则EF的长;
(1)、若 , 如图1,则EF的长;(2)、若 , 如图2,则EF的长;(3)、若 , 如图3,则EF的长;……
(4)、根据上述规律,若 , 则EF的长 , 并证明你的猜想.22. 某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作.已知该品牌运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:第1天
第2天
第3天
第4天
售价x(元/双)
150
200
250
300
销售量y(双)
40
30
24
20
(1)、观察表中数据,x,y满足什么函数关系?写出用x表示y的函数表达式;(2)、若商场计划每天的销售利润为3000元,则每双运动鞋的售价应定为多少元?23. 如图,在 中,过点C作 ,垂足为点D,过点D分别作 , ,垂足分别为 .连接 交线段 于点O.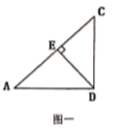
 (1)、在图一 中, , ,有几组相似的三角形,请写出来;(2)、在图二中,证明: ;(3)、如果 , ,试求 的值.
(1)、在图一 中, , ,有几组相似的三角形,请写出来;(2)、在图二中,证明: ;(3)、如果 , ,试求 的值.