安徽省宿州市泗县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 一元二次方程 $x^{2} = 2 x$ 的根是（）

A、 $x = 2$ B、 $x = 0$ C、 $x_{1} = 0, x_{2} = 2$ D、 $x_{1} = 0, x_{2} = - 2$

查看试题解析
2. 下列命题中，真命题的个数有（）个
①有一个角为 $60 °$ 的三角形是等边三角形；②底边相等的两个等腰三角形全等；③有一个内角是 $50 °$ 且腰长相等的两个等腰三角形全等；④一边上的中线等于这条边的一半的三角形是直角三角形．

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 小亮、小莹、大刚三位同学随机地站成一排合影留念，小亮恰好站在中间的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{6}$

查看试题解析
4. 如图， $A B$ 是河堤横断面的迎水坡，坡高 $A C = 1$ ，水平距离 $B C = \sqrt{3}$ ，则斜坡 $A B$ 的坡度为（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\sqrt{3}$ C、 $30 °$ D、 $60 °$

查看试题解析
5. 在平行投影下，矩形的投影不可能是（）

A、 B、 C、 D、

查看试题解析
6. 如图，在矩形 $A B C D$ ，对角线 $A C$ 与 $B D$ 相交于点 $O$ ， $E O ⊥ A C$ 于点O，交 $B C$ 于点E，若 $Δ A B E$ 的周长为8， $A B = 3$ ，则 $A D$ 的长为（）

A、2 B、5.5 C、5 D、4

查看试题解析
7. 如图，半径为13的 $⊙ O$ 内有一点 $A$ ， $O A = 5$ ，点 $P$ 在 $⊙ O$ 上，当 $∠ O P A$ 最大时， $S_{Δ O P A}$ 等于（）

A、40 B、45 C、30 D、65

查看试题解析
8. 如图所示，王华晚上由路灯A下的B处走到C处时，测得影子CD的长为1米，继续往前走3米到达E处时，测得影子EF的长为2米，已知王华的身高是1.5米，那么路灯A的高度AB等于（）

A、4.5米 B、6米 C、7.2米 D、8米

查看试题解析
9. 已知反比例函数y＝﹣ $\frac{12}{x}$ ，当y≤4时，自变量x的取值范围为（　　）

A、x≥3或x＜0 B、x＞0或x≤﹣3 C、x≤﹣3 D、x≥3

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c$ (a≠0)的图象如图所示，对称轴是直线x=1，下列结论：①2a＋b=0；②abc＜0；③9a＋3b＋c＞0；④3a＋c＜0；⑤若m≠1，则m(am＋b)－a＜b．其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 电影《长津湖》首映当日票房已经达到2.06亿元，2天后当日票房达到4.38亿元，设平均每天票房的增长率为x，则可列方程为．

查看试题解析
12. 如果 $| 1 - \tan α | + {(\sin β - \frac{1}{2})}^{2} = 0$ （ $α 、 β$ 为锐角），则 $α =$ ， $β =$ .

查看试题解析
13. 二次函数 $y = 2 x^{2} - 8 x + 7$ 的顶点坐标为．

查看试题解析
14. 已知：如图，在 $R t △ A B C$ 中，点 $D_{1}$ 是斜边 $A B$ 的中点，过点 $D_{1}$ 作 $D_{1} E_{1} ⊥ A C$ 于点 $E_{1}$ ，连接 $B E_{1}$ 交 $C D_{1}$ 于点 $D_{2}$ ；过点 $D_{2}$ 作 $D E_{2} ⊥ A C$ 于点 $E_{2}$ ，连接 $B E_{2}$ 交 $C D_{1}$ 于点 $D_{3}$ ；过点 $D_{3}$ 作 $D_{3} E_{3} ⊥ A C$ 于点 $E_{3}$ ， …，如此继续，可以依次得到点 $D_{4}$ ， $D_{5}$ ， …， $D_{n}$ ，分别记 $△ B D_{1} E_{1}$ ， $△ B D_{2} E_{2}$ ， $△ B D_{3} E_{3}$ ， …， $△ B D_{n} E_{n}$ 的面积为 $S_{1}$ ， $S_{2}$ ， $S_{3}$ ， …， $S_{n}$ 设 $△ A B C$ 的面积为1，则 $S_{n} =$ （用含n的代数式表示）.

查看试题解析

三、解答题

15. 计算：

(1)、解方程： $4 x^{2} + 1 = 4 x$ ；

(2)、 $s i n^{2} 6 0^{°} + c o s^{2} 6 0^{°} - t a n 4 5^{°}$

查看试题解析
16. 今年是中国共产党建党100周年，中华人民共和国成立72周年！在国庆前夕，社区便民超市调查了某种水果的销售情况获得如下信息：
信息一：进价是每千克12元；

信息二：当销售价为每千克27元时，每天可售出120千克；

若每千克售价每降低2元，则每天的销售量将增加80千克．根据以上信息解答问题：该超市每天想要获得3080元的销售利润，又要尽可能让顾客得到实惠，求这种水果的销售单价应为多少元．

查看试题解析
17. 已知，平面直角坐标系中， $△ A B C$ 的位置如图所示，点A、B、C的坐标分别为 $(1 ， 0)$ 、 $(4 ， - 1)$ 、 $(3 ， 2)$ ． $△ A_{1} B_{1} C_{1}$ 与 $△ A B C$ 是以点P为位似中心的位似图形；

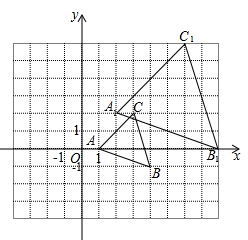(1)、请画出点P的位置，井写出点P的坐标；

(2)、请以点O为位似中心在y轴左侧，画出 $△ A B C$ 的位似图形 $△ A_{2} B_{2} C_{2}$ ，使相似比为 $1 ： 1$ ，若点 $M (a ， b)$ 为 $△ A B C$ 内一点，则点M在 $△ A_{2} B_{2} C_{2}$ 内的对应点的坐标为．

查看试题解析
18. 如图，在△ABC中，AD是BC边上的中线，点E是AD的中点，过点A作AF∥BC交BE的延长线于F，连接CF．

(1)、求证：△AEF≌△DEB；

(2)、若∠BAC＝90°，试判断四边形ADCF的形状，并证明你的结论．

查看试题解析
19. 如图，AB是⊙O的直径，弦CD⊥AB于点E，点M在⊙O上，MD经过圆心O，连接MB．

(1)、若CD＝16，BE＝4，求⊙O的半径；

(2)、若∠M＝∠D，求∠D的度数．

查看试题解析
20. 如图， $Δ A O B$ 为等腰直角三角形，斜边 $O B$ 在x轴上，一次函数 $y = 3 x - 4$ 的图象经过点A，交y轴于点C，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图像也经过点A．

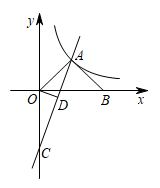(1)、求反比例函数的解析式；

(2)、过O点作 $O D ⊥ A C$ 于 $D$ 点，求 $C D^{2} - A D^{2}$ 的值．

查看试题解析
21. 从2020年1月至今，新冠肺炎疫情逐渐蔓延开来．成都某学校为了增强学生的防新冠肺炎的意识，做到科学防护．在七八年级组织开展了“疫情防控，我们在行动”相关知识竞答活动，学校对知识竞答获奖者的获奖情况进行了统计，并绘制了如图两幅完整的统计图．请结合统计图中的信息，解决下列问题．

(1)、在这次比赛中，七、八年级一共有人获奖；

(2)、请补全条形统计图，在扇形统计图中，三等奖所对的圆心角 $α$ ＝；

(3)、获得特等奖的同学中，有3人来自八年级，3人中2人是女生．现在准备从八年级获得特等奖的3名同学中任选两名参加市级防疫知识竞答活动，请用列表法或者树状图的方法，求恰好选中一名男生一名女生参加市级防疫知识竞答活动的概率．

查看试题解析
22. 2022年北京冬奥会即将召开，激起了人们对冰雪运动的极大热情．如图是某跳台滑雪训练场的横截面示意图，取某一位置的水平线为x轴，过跳台终点A作水平线的垂线为y轴，建立平面直角坐标系，图中的抛物线 $C_{1} ： y = - \frac{1}{5} x^{2} + 2 x + 1$ 近似表示滑雪场地上的一座小山坡，某运动员从点O正上方4米处的A点滑出，滑出后沿一段抛物线 $C_{2} ： y = - \frac{1}{4} x^{2} + b x + c$ 运动．

(1)、求山坡坡顶的高度；

(2)、当运动员运动到离A处的水平距离为2米时，离水平线的高度为7米，求抛物线 $C_{2}$ 的函数解析式（不要求写出自变量x的取值范围）；

(3)、在（2）的条件下，当运动员运动的水平距离为多少米时，运动员与小山坡的竖直距离为1米？

查看试题解析
23. 在 $Δ A B C$ 中， $∠ A C B = 4 5^{°}$ ，点D（与点 $B 、 C$ 不重合）为射线 $B C$ 上一动点，连接 $A D$ ，以 $A D$ 为一边且在 $A D$ 的右侧作正方形 $A D E F$ ．

(1)、如果 $A B = A C$ ．如图①，且点D在线段 $B C$ 上运动．试判断线段 $C F$ 与 $B D$ 之间的位置关系，并证明你的结论．

(2)、如果 $A B > A C$ ，如图②，且点D在线段 $B C$ 上运动．（1）中结论是否成立，为什么？

(3)、若正方形 $A D E F$ 的边 $D E$ 所在直线与线段 $C F$ 所在直线相交于点P，设 $A C = 4 \sqrt{2}$ ， $B C = 3$ ， $B D = x$ ，求线段 $C P$ 的长．（用含x的式子表示）．

查看试题解析