安徽省合肥市瑶海区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 在反比例函数 $y = \frac{k + 1}{x}$ 的图象的每一个分支上，y都随x的减小而增大，则k的取值范围是（）

A、 $k > 0$ B、 $k < 0$ C、 $k > - 1$ D、 $k < - 1$

查看试题解析
2. 如图， $A B$ // $C D$ // $E F$ ， $B E$ 与 $A F$ 相交于点H，且 $A H = 2 H D = \frac{1}{2} D F$ ，则 $\frac{B C}{C E}$ 的值为（）

A、1 B、 $\frac{3}{4}$ C、 $\frac{2}{3}$ D、 $\frac{5}{6}$

查看试题解析
3. 在Rt $△ A B C$ 中， $∠ C = 90 °$ ，若 $c o s A = \frac{12}{13}$ ，则 $t a n B$ 的值为（）

A、 $\frac{5}{13}$ B、 $\frac{13}{5}$ C、 $\frac{12}{5}$ D、 $\frac{5}{12}$

查看试题解析
4. 如图，在 $⊙ O$ 中， $O E ⊥$ 弦 $A B$ 于点E， $E O$ 的延长线交弦 $A B$ 所对的优弧于点F．若 $A B = F E = 8$ ，则 $⊙ O$ 的半径为（）

A、5 B、6 C、4 D、 $2 \sqrt{5}$

查看试题解析
5. 若一个矩形剪掉一个面积最大的正方形，剩下的小矩形与原来的矩形相似，且原矩形的较长边长为 $8 c m$ ，则剩下的小矩形的较短边长为（）

A、 $2 \sqrt{5}$ B、 $5 \sqrt{5} - 8$ C、 $4 \sqrt{5} - 4$ D、 $12 - 4 \sqrt{5}$

查看试题解析
6. 如图， $△ A B C$ 与 $△ D E F$ 位似，点O是位似中心．若 $O A ： A D = 2 ： 3$ ， $△ D E F$ 与 $△ A B C$ 的周长差为 $12 c m$ ，则 $△ A B C$ 的周长为（）

A、 $6 c m$ B、 $8 c m$ C、 $10 c m$ D、 $12 c m$

查看试题解析
7. $B D$ 是Rt $△ A B C$ 的斜边 $A C$ 上的高， $∠ A \neq 45 °$ ，下列比值中与 $s i n A$ 不相等的是（）

A、 $\frac{B C}{A C}$ B、 $\frac{C D}{B C}$ C、 $\frac{B D}{A B}$ D、 $\frac{B D}{B C}$

查看试题解析
8. 若二次函数 $y = x^{2} + 2 x - m$ 的图象与坐标轴有三个交点，则m的取值范围是（）

A、 $m > - 1$ 且 $m \neq 0$ B、 $m < 1$ 且 $m \neq 0$ C、 $m > - 1$ D、 $m < 1$

查看试题解析
9. 如图，将 $△ A B C$ 绕点A逆时针旋转至 $△ A B^{'} C^{'}$ 的位置，连接 $B B^{'}$ ，若 $∠ B A C = 18 °$ ， $∠ A B B^{^{'}} = 67 °$ ，则 $∠ C A B^{'}$ 的度数为（）

A、25° B、30° C、28° D、32°

查看试题解析
10. 如图，一条抛物线（形状一定）与x轴相交于E、F两点（点E在点F左侧），其顶点P在线段 $A B$ 上移动．若点A、B的坐标分别为 $(- 2 ， - 3)$ 、 $(4 ， - 3)$ ，点E的横坐标的最小值为-5，则点F的横坐标的最大值为（）

A、6 B、7 C、8 D、9

查看试题解析

二、填空题

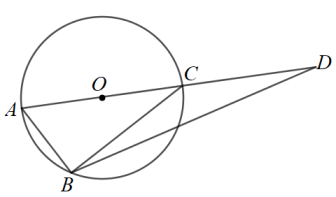
11. 某人沿着坡角为 $α$ 的斜坡前进80m，则他上升的最大高度是m．

查看试题解析
12. 如图， $A B$ 、 $B C$ 是以 $A C$ 为直径的 $⊙ O$ 的两条弦，延长 $A C$ 至点D，使 $C D = B C$ ，则当 $∠ D = 15 °$ 时， $A D$ 与 $A B$ 之间的数量关系为： $A D =$ $A B$ ．

查看试题解析
13. 已知抛物线 $y = x^{2} - 6 x + 8$ 的顶点为P，与x轴相交于M，N两点（点M在点N左侧），平移此抛物线，使点P平移后的对应点 $P^{'}$ 落在x轴上，点M平移后的对应点 $M^{'}$ 落在y轴上，则平移后的抛物线解析式为．

查看试题解析
14. 如图， $A D$ 是 $△ A B C$ 的中线，E是 $A D$ 上一点，且 $A D = 4 A E$ ．连接 $B E$ 并延长交 $A C$ 于点F，过点A作 $A G$ // $B C$ 交 $B F$ 的延长线于点G，则 $\frac{G F}{B E} =$ ．

查看试题解析

三、解答题

15. 一个二次函数，当 $x = - 1$ 时，函数的最大值为2，它的图像经过点 $(1 ， 6)$ ，求这个二次函数的表达式．

查看试题解析
16. 如图， $A B$ // $C D$ ， $A D ⊥ B C$ 于点O， $O A = 6$ ， $O D = 9$ ， $B C = 10$ ，求 $C D$ 的长．

查看试题解析
17. 如图， $A C$ ， $B C$ 是 $⊙ O$ 的两条弦，且 $A C = B C$ ， $∠ A O C + ∠ A B C = 75 °$ ， D为弦 $A B$ 所对优弧上一点，求 $∠ D$ 的度数．

查看试题解析
18. 如图，等腰Rt $△ O A B$ 的直角顶点A在反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象上．

(1)、已知 $O A = 2 \sqrt{2}$ ，求此反比例函数的解析式；

(2)、先将点A绕原点O逆时针旋转90°，得到点E，再将点E向右平移1个单位得到点F，若点F恰好在正比例函数 $y = m x$ 的图象上，求正比例函数 $y = m x$ 的表达式．

查看试题解析
19. 如图，热气球的探测器显示，从热气球看一栋大楼顶部的仰角 $α$ 为30°，看这栋大楼底部上方3m处点E的俯角 $β$ 为60°，热气球与大楼的水平距离为80m，求这栋大楼的高度（结果保留整数）．（参考数据： $\sqrt{2} \approx 1.414$ ， $\sqrt{3} \approx 1.732$ ）

查看试题解析
20. 如图， $⊙ O$ 与 $R t △ A B C$ 的一条直角边 $B C$ 相交于点D，与另一条直角边 $A C$ 相切于点E，过点E作 $E F ⊥ A B$ 于点F，求证： $E C = E F$ ．

查看试题解析
21. 已知 $y = 2 x + b$ 是关于x的一次函数．

(1)、当b为何值时，一次函数 $y = 2 x + b$ 的图象与二次函数 $y = x^{2} - 2 x + 4$ 的图象只有一个公共点？

(2)、若一次函数 $y = 2 x + b$ 的图象与二次函数 $y = x^{2} - 2 x + 4$ 的图象有两个公共点，且其中一个公共点恰是该二次函数图象的顶点，求另一个公共点的坐标；

(3)、在（2）的条件下，直接写出当二次函数值大于一次函数值时x的取值范围．

查看试题解析
22. 已知：如图，在 $△ A B C$ 中， $A D$ 是 $B C$ 边上的高．在这个三角形内有一个内接矩形 $P Q M N$ ，矩形的一边在 $B C$ 上，另两个顶点分别在 $A B$ ， $A C$ 上．

(1)、若 $B C = 60$ ， $A D = 40$ ，当 $P Q = P N$ 时，求 $P Q$ 的长；

(2)、若 $B C = 100$ ， $A D = 40$ ，当 $P Q = P N$ 且 $∠ B A C = 90 °$ 时，直接写出 $B N \cdot C M$ 的值；

(3)、若 $B C = 60$ ， $A D = 40$ ，当矩形 $P Q M N$ 的面积最大时，求这个矩形的边长．

查看试题解析
23. 已知： $∠ B A C$ 为钝角， $B E$ ， $C F$ 是 $△ A B C$ 的两条高．

(1)、如图1，若 $A B = A C$ ，求证： $A E = A F$ ；

(2)、如图2，若 $A B \neq A C$ ，延长 $B E$ 、 $C F$ 相交于点O，连接 $E F$ ．当 $O E = 4$ ， $E F = 6$ ， $O C = 10$ 时，求 $B C$ 的长；

(3)、如图3，若 $A B \neq A C$ ，延长 $B E$ 、 $C F$ 相交于点O，连接 $E F$ ．当 $S_{△ A B E} = \frac{6}{5} S_{△ A B C} = 4 S_{△ A C F}$ 时，求 $\frac{E F}{B C}$ 的值．

查看试题解析