安徽省合肥市庐阳区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-10-09 类型:期末考试
一、单选题
-
1. 已知 , 那么下列等式中,不成立的是( )A、 B、 C、 D、2. 若反比例函数 的图象经过点(1,-2),则k=( )A、 B、2 C、 D、3. 观察如图所示的正五角星,下列说法正确的是( )
 A、既是轴对称图形,也是中心对称图形 B、不是轴对称图形,是中心对称图形 C、不是中心对称图形,是轴对称图形 D、既不是轴对称图形,也不是中心对称图形4. 已知:Rt中, , , , 则的值为( )A、 B、 C、 D、5. 如图,A、B、C分别是双曲线(x<0)与(x>0)及x轴上的点,AB//x轴,△ABC的面积为2,则k的值是( )
A、既是轴对称图形,也是中心对称图形 B、不是轴对称图形,是中心对称图形 C、不是中心对称图形,是轴对称图形 D、既不是轴对称图形,也不是中心对称图形4. 已知:Rt中, , , , 则的值为( )A、 B、 C、 D、5. 如图,A、B、C分别是双曲线(x<0)与(x>0)及x轴上的点,AB//x轴,△ABC的面积为2,则k的值是( )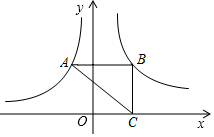 A、 B、 C、 D、6. 如图,中,点D是边上一点,下列条件中,不能判定与相似的是( )
A、 B、 C、 D、6. 如图,中,点D是边上一点,下列条件中,不能判定与相似的是( )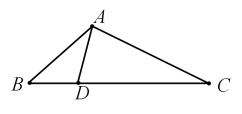 A、 B、 C、 D、7. 已知抛物线 , 过 , 且对称轴是直线 , 则当时,自变量x的取值范围是( )A、 B、 C、 D、或8. 中 , B为弧中点,// , 则度数为( )
A、 B、 C、 D、7. 已知抛物线 , 过 , 且对称轴是直线 , 则当时,自变量x的取值范围是( )A、 B、 C、 D、或8. 中 , B为弧中点,// , 则度数为( )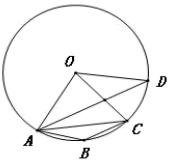 A、20° B、30° C、40° D、45°9. 对于抛物线y=﹣(x+2)2+3,下列结论中正确结论的个数为( )
A、20° B、30° C、40° D、45°9. 对于抛物线y=﹣(x+2)2+3,下列结论中正确结论的个数为( )①抛物线的开口向下; ②对称轴是直线x=﹣2;
③图象不经过第一象限; ④当x>2时,y随x的增大而减小.
A、4 B、3 C、2 D、110. 如图,在矩形中, , , P是射线上动点,E在射线上, . 点P从C点运动,设 , , 则能反映y与x之间函数关系的图象是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 已知线段b是线段a、c的比例中项,且 , , 那么b= .12. 某物体沿着坡比为4∶3的坡面上升了8米,那么在坡面上移动了米.13. 如图是由边长为1的小正方形组成的网格,则 .
 14. 等腰直角中, , , 点D是平面内一点, , 连接 , 将绕D点逆时针旋转90°得到 , 连接 , 当(填度数)度时,可以取最大值,最大值等于 .
14. 等腰直角中, , , 点D是平面内一点, , 连接 , 将绕D点逆时针旋转90°得到 , 连接 , 当(填度数)度时,可以取最大值,最大值等于 .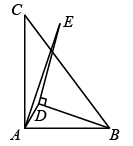
三、解答题
-
15. 计算:16. 如图,学校某处空地上有A、B、C三棵树,现准备建一个圆形景观鱼池,要求A、B、C三棵树恰在圆周上,请你帮助设计鱼池,在图中作出它的鱼池轮廓,保留作图痕迹并将圆心标记为点O.
 17. 如图是一个的正方形网格和平面直角坐标系,网格的每个小正方形边长为l,顶点都为格点的三角形我们称作格点三角形.如图是格点三角形.
17. 如图是一个的正方形网格和平面直角坐标系,网格的每个小正方形边长为l,顶点都为格点的三角形我们称作格点三角形.如图是格点三角形.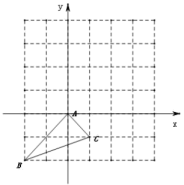 (1)、将绕点A顺时针旋转90°,得到对应图形;(2)、在网格中,以B为位似中心,同侧将按2:1放大,对应得到 , 画出 , 直接写出点坐标.18. 如图,直线与双曲线在第一象限内交于A、B两点,已知 , .
(1)、将绕点A顺时针旋转90°,得到对应图形;(2)、在网格中,以B为位似中心,同侧将按2:1放大,对应得到 , 画出 , 直接写出点坐标.18. 如图,直线与双曲线在第一象限内交于A、B两点,已知 , . (1)、求直线和双曲线解析式:(2)、根据图象直接写出不等式的解集.19. 如图,数学兴趣小组为测量旗杆和教学楼的高,先在E处用高1.5米的测角仪测得教学楼顶端A的仰角为45°,此时旗杆顶端D恰好在视线上,再向前走12米在G处(G在上),又测得教学楼顶端A的仰角为60°,点B、C、E三点在同一水平线上.
(1)、求直线和双曲线解析式:(2)、根据图象直接写出不等式的解集.19. 如图,数学兴趣小组为测量旗杆和教学楼的高,先在E处用高1.5米的测角仪测得教学楼顶端A的仰角为45°,此时旗杆顶端D恰好在视线上,再向前走12米在G处(G在上),又测得教学楼顶端A的仰角为60°,点B、C、E三点在同一水平线上. (1)、求旗杆的高;(2)、求教学楼的高(结果用准确值表示).20. 如图,线段是圆O的直径,O是圆心,C、D是圆上的点,且// . 过点O作于点E,交于点F.若 , , 求的长.
(1)、求旗杆的高;(2)、求教学楼的高(结果用准确值表示).20. 如图,线段是圆O的直径,O是圆心,C、D是圆上的点,且// . 过点O作于点E,交于点F.若 , , 求的长. 21. 如图, , , 一抛物线顶点为 , 且过A、B两点.C,D是抛物线上且位于x轴上方的点,//轴,轴于点E,轴于点F.
21. 如图, , , 一抛物线顶点为 , 且过A、B两点.C,D是抛物线上且位于x轴上方的点,//轴,轴于点E,轴于点F. (1)、求抛物线解析式;(2)、若四边形是正方形,求的值.22. 某超市以10元/个的价格购进一批新型儿童玩具,当以17元/个的价格出售时,每天可以售出50个.春节期间,在确保不亏本的前提下采取降价促销的方式招揽顾客,经调查发现,当售价每降低0.5元时,每天可多卖出5个玩具.(1)、设该玩具的售价降低了x元,每天的销售量为y个,直接写出y与x的函数关系式及自变量x的取值范围.(2)、设销售这种玩具一天可获利润为w元,求w与x之间的函数关系式.(3)、这种玩具的售价定为每个多少元时,商店每天获得的利润最大?23. 中, , , 点E为边上一点,点D为延长线上一点, , 连接、 , 并延长交于F,设 .
(1)、求抛物线解析式;(2)、若四边形是正方形,求的值.22. 某超市以10元/个的价格购进一批新型儿童玩具,当以17元/个的价格出售时,每天可以售出50个.春节期间,在确保不亏本的前提下采取降价促销的方式招揽顾客,经调查发现,当售价每降低0.5元时,每天可多卖出5个玩具.(1)、设该玩具的售价降低了x元,每天的销售量为y个,直接写出y与x的函数关系式及自变量x的取值范围.(2)、设销售这种玩具一天可获利润为w元,求w与x之间的函数关系式.(3)、这种玩具的售价定为每个多少元时,商店每天获得的利润最大?23. 中, , , 点E为边上一点,点D为延长线上一点, , 连接、 , 并延长交于F,设 .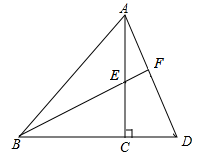 (1)、求证:;(2)、若F恰好是中点,求x的值;(3)、设 , 当时,求y的值.
(1)、求证:;(2)、若F恰好是中点,求x的值;(3)、设 , 当时,求y的值.