安徽省合肥市高新区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形是我国国产品牌汽车的标识，这些汽车标识中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 某斜坡的坡度 $i = 1 ： \sqrt{3}$ ，则该斜坡的坡角为（　　）

A、75° B、60° C、45° D、30°

查看试题解析
3. 将抛物线y＝﹣3x²﹣1向左平移2个单位长度，再向下平移2个单位长度，所得到的抛物线为（　　）

A、y＝﹣3（x+2）²+1 B、y＝﹣3（x﹣2）²﹣3 C、y＝﹣3（x+2）²﹣3 D、y＝﹣3（x﹣2）²+1

查看试题解析
4. 如图，在△ABC中，∠C＝90°，若sinB＝ $\frac{4}{5}$ ，则sinA＝（　　）

A、 $\frac{3}{5}$ B、 $\frac{3}{4}$ C、 $\frac{4}{5}$ D、 $\frac{4}{3}$

查看试题解析
5. 若反比例函数y= $\frac{1 - 2 k}{x}$ 的图象分布在第二、四象限，则k的取值范围是（）

A、k< $\frac{1}{2}$ B、k> $\frac{1}{2}$ C、k>2 D、k<2

查看试题解析
6. 如图，在△ABC中，点D、E和点F、G分别是边AB、AC的三等分点，△ABC的面积为18，则四边形DEGF的面积为（　　）

A、2 B、3 C、6 D、9

查看试题解析
7. 如图，CD是Rt△ABC斜边AB上的中线，过点C作CE⊥CD交AB的延长线于点E，添加下列条件仍不能判断△CEB与△CAD相似的是（　　）

A、∠CBA＝2∠A B、点B是DE的中点 C、CE•CD＝CA•CB D、 $\frac{C E}{C A}$ ＝ $\frac{B E}{A D}$

查看试题解析
8. 如图，四边形 $A B C D$ 是半圆的内接四边形， $A B$ 是直径， $\overset{⌢}{D C} = \overset{⌢}{C B}$ .若 $∠ C = 110 °$ ，则 $∠ A B C$ 的度数等于（）

A、 $55 °$ B、 $60 °$ C、 $65 °$ D、 $70 °$

查看试题解析
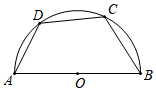9. 如图，抛物线y＝ax²+bx+c（a≠0）的对称轴为直线x＝1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示．下列结论中正确的个数有（　　）个．
①abc＞0；
②方程ax²+bx+c＝0的两个根是x₁＝﹣1，x₂＝3；
③3a+c＞0；
④当ax²+bx+c＞3时，x的取值范围是0＜x＜2．

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 已知二次函数y＝﹣x²+2x+3，截取该函数图象在0≤x≤4间的部分记为图象G，设经过点（0，t）且平行于x轴的直线为l，将图象G在直线l下方的部分沿直线l翻折，图象G在直线上方的部分不变，得到一个新函数的图象M，若函数M的最大值与最小值的差不大于5，则t的取值范围是（　　）

A、﹣1≤t≤0 B、﹣1≤t $\leq - \frac{1}{2}$ C、 $- \frac{1}{2} \leq t \leq 0$ D、t≤﹣1或t≥0

查看试题解析

二、填空题

11. 二次函数y＝x²－2x＋m的图象与x轴的一个交点的坐标是（－1，0），则图像与x轴的另一个交点的坐标是．

查看试题解析
12. 如图，在 $△ A B C$ 中， $∠ A C B = 90^{°}$ ，且 $A C = B C$ .点D是 $△ A B C$ 内的一点，将 $△ A C D$ 以点C为中心顺时针旋转 $90^{°}$ 得到 $△ B C E$ ，若点A、D、E共线，则 $∠ A E B$ 的度数为.

查看试题解析
13. 如图，在平面直角坐标系中，直线y＝﹣ $\frac{1}{2}$ x与反比例函数 $y = \frac{k}{x}$ （x＜0）的图象交于点A（﹣2，m），将直线y＝﹣ $\frac{1}{2}$ x沿y轴向上平移n个单位长度，交y轴于点B，交反比例函数图象于点C，连接OC，若BC＝ $\frac{1}{2}$ OA，则n的值为．

查看试题解析
14. 四边形ABCD是一张矩形纸片，点E在AD上，将△ABE沿BE折叠，使点A落在矩形的对角线BD上，连接CF，若DE＝1，请探究下列问题：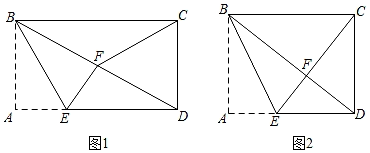

(1)、如图1，当F恰好为BD的中点时，AE＝；

(2)、如图2，当点C、E、F在同一条直线上时，AE＝．

查看试题解析

三、解答题

15. 计算：（3﹣π）⁰﹣2cos30°﹣ $\sqrt{12}$ +|1﹣tan60°|．

查看试题解析
16. 如图，在平面直角坐标系中，△ABC的顶点均在格点（网格线的交点）上．
( 1 )将△ABC绕点A顺时针旋转90°得到△AB₁C₁ ，画出△AB₁C₁；
( 2 )在给定的网格中，以点O为位似中心，将△ABC放大为原来的2倍，得到△A₂B₂C₂ ，画出△A₂B₂C₂ ．

查看试题解析
17. 已知二次函数y＝﹣ $\frac{1}{2}$ x²+bx+c的图象如图所示，它与x轴的一个交点坐标为（1，0），与y轴的交点坐标为（0，1）．

(1)、求此二次函数的表达式；

(2)、用配方法求顶点坐标．

查看试题解析
18. 已知，如图：AB是⊙O的直径，AB＝AC，BC交⊙O于D，DE⊥AC于点E，求证：DE是⊙O的切线．

查看试题解析
19. 小聪在学习解直角三角形的知识后，萌生了测量他家对面位于同一水平面的楼房高度的想法，他站在自家C处测得对面楼房顶端A的仰角为37°，然后又下楼至楼底的D处，测得对面楼房顶端A的仰角为60°，已知CD的距离为40米，请你用小聪测得的数据求出对面楼房AB的高度．（结果精确到0.1米，参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75， $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73）

查看试题解析
20. 如图，已知Rt△ABC中，∠BAC＝90°，BC＝6，AC＝4 $\sqrt{2}$ ，以A为圆心，AB为半径画圆，与边BC交于另一点D．

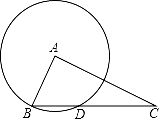(1)、求BD的长；

(2)、连接AD，求∠DAC的余弦值．

查看试题解析
21. 如图，一次函数y＝kx+b的图象与反比例函数y＝ $\frac{4}{x}$ （x＞0）的图象交于A（m，4）、B（2，n）的两点，与坐标轴分别交于M、N两点．

(1)、求一次函数的解析式；

(2)、根据图象，直接写出不等式kx+b﹣ $\frac{4}{x}$ ＜0的解集；

(3)、求△AOB的面积．

查看试题解析
22. 某大学生利用暑假40天社会实践参与了某公司旗下一家加盟店经营，了解到一种成本为20元/件的新型商品在第 $x$ 天销售的相关信息如下表所示：

销售量 $p$ （件）

$p = 50 - x$

销售单价 $q$ （元/件）

当 $1 \leq x \leq 20$ 时， $q = 30 + \frac{1}{2} x$

当 $21 \leq x \leq 40$ 时， $q = 20 + \frac{525}{x}$

(1)、请计算第几天该商品的销售单价为35元/件；

(2)、这40天中该加盟店第几天获得的利润最大？最大利润是多少？

(3)、在实际销售的前20天中，公司为鼓励加盟店接收大学生参加实践活动决定每销售一件商品就发给该加盟店 $m (m \geq 2)$ 元奖励，通过该加盟店的销售记录发现，前10天中，每天获得奖励后的利润随时间 $x$ （天）的增大而增大，求 $m$ 的取值范围.

查看试题解析
23. 如图①，在正方形ABCD中，B为边BC上一点，连接AE，过点D作DN⊥AE交AE、AB分别于点F、N．

(1)、求证：△ABE≌△DAN；

(2)、若E为BC中点，
①如图②，连接AC交DP于点M，求CM：AM的值；
②如图③，连接CF，求tan∠CFE的值．

查看试题解析