安徽省合肥市肥西县2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-10-09 类型:期末考试
一、单选题
-
1. 抛物线的顶点坐标是( )A、 B、 C、 D、2. 若反比例函数的图象经过点(2,4),则k的值是( )A、 B、 C、 D、3. 在中, , 若的三边都缩小5倍,则的值( )A、放大5倍 B、缩小5倍 C、不变 D、无法确定4. 等腰三角形底边与底边上的高的比是2: ,则它的顶角为( )A、30° B、45° C、60° D、120°5. 下列各组的四条线段 , , , 是成比例线段的是( )A、 , , , B、 , , , C、 , , , D、 , , ,6. 如图,在△ABC中,D、E分别是AB、AC上的点,DE∥BC,BE与CD相交于F,则下列结论一定正确的是( ).
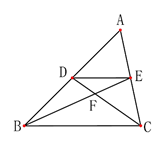 A、 B、 C、 D、7. 抛物线 上部分点的横坐标x,纵坐标y的对应值如下表:
A、 B、 C、 D、7. 抛物线 上部分点的横坐标x,纵坐标y的对应值如下表:x
…
0
1
2
…
y
…
0
4
6
6
4
…
从上表可知,下列说法正确的个数是( )
①抛物线与x轴的一个交点为 ②抛物线与y轴的交点为
③抛物线的对称轴是:直线 ④在对称轴左侧y随x的增大而增大
A、1 B、2 C、3 D、48. 如图,在△ABC中,∠BAC=120°,AC=8,AB=4,则BC的长是( ) A、 B、 C、6 D、89. 如图,点P是△ABC的边AC上一点,连结BP , 以下条件中,不能判定△ABP∽△ACB的是( )
A、 B、 C、6 D、89. 如图,点P是△ABC的边AC上一点,连结BP , 以下条件中,不能判定△ABP∽△ACB的是( ) A、 = B、 = C、∠ABP=∠C D、∠APB=∠ABC10. 如图,Rt△OAB中,∠OAB=90°,点A在x轴上,反比例函数y=(x>0)的图象过斜边OB的中点D,与AB交于点C.若△OBC的面积为3,则k的值是( )
A、 = B、 = C、∠ABP=∠C D、∠APB=∠ABC10. 如图,Rt△OAB中,∠OAB=90°,点A在x轴上,反比例函数y=(x>0)的图象过斜边OB的中点D,与AB交于点C.若△OBC的面积为3,则k的值是( )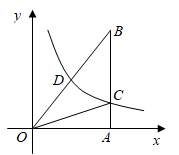 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 比较大小:sin48°cos48°(填“>”、“<”或“=”).12. 若= , 则的值为 .13. 把抛物线y=x2先向右平移2个单位,再向上平移3个单位,平移后抛物线的表达式是 .
14. 若点都在反比例函数的图象上,则的从小到大的关系是 .15. 如果正方形 的边长为4, 为 边上一点, , 为线段 上一点,射线 交正方形的一边于点 ,且 ,那么 的长为 .三、解答题
-
16. 计算:sin30°+cos60°﹣tan45°•tan60°.17. 如图,在平面直角坐标系中,的三个顶点坐标分别为 , , .
 (1)、以原点O为位似中心,在第二象限内画出将放大为原来的2倍后的;(2)、分别写出 , , 三个点的坐标.18. “南水北调工程”(中线)有一段堤坝如图所示,其横断面为梯形ABCD,高米,斜坡CD的坡度是1∶1,但是,为了建设高铁线路,电力部门要在堤坝的正上方通过一组高压线,且高压线的最低点P与点D,H在同一条直线上(), .
(1)、以原点O为位似中心,在第二象限内画出将放大为原来的2倍后的;(2)、分别写出 , , 三个点的坐标.18. “南水北调工程”(中线)有一段堤坝如图所示,其横断面为梯形ABCD,高米,斜坡CD的坡度是1∶1,但是,为了建设高铁线路,电力部门要在堤坝的正上方通过一组高压线,且高压线的最低点P与点D,H在同一条直线上(), . (1)、求斜坡CD的坡角α.(2)、电力部门要求此处高压线离堤面AD的安全距离不低于18米,则此段大坝是否达到了安全要求?(参考数据: , , , )19. 如图,一次函数的图象与反比例函数的图象交于点、 , 交y轴于点B,交x轴于点D.
(1)、求斜坡CD的坡角α.(2)、电力部门要求此处高压线离堤面AD的安全距离不低于18米,则此段大坝是否达到了安全要求?(参考数据: , , , )19. 如图,一次函数的图象与反比例函数的图象交于点、 , 交y轴于点B,交x轴于点D. (1)、求反比例函数和一次函数的表达式;(2)、连接、 , 求的面积;(3)、直接写出时x的取值范围.20. 凤凰县某超市销售一种大米,每千克大米的成本为5元,经试销发现,该大米每天的销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价、销售量的四组对应值如下表所示:
(1)、求反比例函数和一次函数的表达式;(2)、连接、 , 求的面积;(3)、直接写出时x的取值范围.20. 凤凰县某超市销售一种大米,每千克大米的成本为5元,经试销发现,该大米每天的销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价、销售量的四组对应值如下表所示:销售单价x(元/斤千克)
6
6.5
7
7.5
销售量y(千克)
1000
900
800
700
(1)、求y(千克)与x(元/千克)之间的函数表达式(不要求写出自变量取值范围).(2)、为保证某天获得1600元的销售利润,且要惠及客户,则该天的销售单价应定为多少?(3)、当销售单价定为多少时,才能使当天的销售利润最大?最大利润是多少?21. 如图1,已知四边形ABCD是正方形,点E,F分别在BA,AD的延长线上, ,BF交CD于点O,ED的延长线交BF于点G,连接CG. (1)、求证: ;(2)、求 的度数;(3)、如图2,连接AG,求证: .
(1)、求证: ;(2)、求 的度数;(3)、如图2,连接AG,求证: .