安徽省合肥市包河区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知线段a、b、c满足 $\frac{a}{b} = \frac{b}{c}$ ，其中a=4cm、b=12cm，则c的长度为（）

A、9cm B、18cm C、24cm D、36cm

查看试题解析
3. 已知反比例函数的解析式为y= $- \frac{6}{x}$ ，则它的图象经过点（）

A、（1，3） B、（1，-3） C、（-1，3） D、（-2，3）

查看试题解析
4. 如图，在边长为1的正方形网格中，点A、O、B均在格点上，则tan∠AOB的值是（）

A、 $\frac{1}{2}$ B、2 C、 $\sqrt{5}$ D、 $\frac{\sqrt{5}}{2}$

查看试题解析
5. 将函数y=2x²+4x+1的图象向下平移两个单位，以下结论正确的是（）

A、开口方向改变 B、对称轴位置改变 C、y随x的变化情况不变 D、与y轴的交点不变

查看试题解析
6. 如图，▱BDEF顶点D、E、F分别在△ABC的三边上，则下列比例式不成立的是（）

A、 $\frac{A D}{D B} = \frac{A E}{E C}$ B、 $\frac{A E}{A C} = \frac{D E}{B C}$ C、 $\frac{A D}{E F} = \frac{D E}{F C}$ D、 $\frac{A D}{A B} = \frac{C F}{B F}$

查看试题解析
7. 如图，在离铁塔BC底部30米的D处，用测角仪从点A处测得塔顶B的仰角为α＝30°，测角仪高AD为1.5米，则铁塔的高BC为（）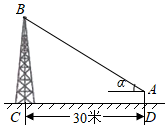

A、16.5米 B、（10 $\sqrt{3}$ ＋1.5）米 C、（15 $\sqrt{3}$ ＋1.5）米 D、（15 $\sqrt{2}$ ＋1.5）米

查看试题解析
8. 如图，四边形ABCD内接于⊙O，若∠AOB=40°，BC∥OA，则∠ADC的度数为（）

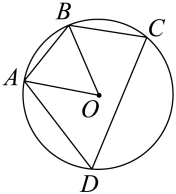A、60° B、65° C、70° D、75°

查看试题解析
9. 在体育选项报考前，某九年级学生对自己某次实心球训练的录像进行分析，发现实心球飞行高度y(米)与水平距离x(米)之间的关系为y= $- \frac{1}{12} x^{2} + \frac{2}{3} x + \frac{5}{3}$ ，由此可知该生此次实心球训练的成绩为（）

A、6米 B、10米 C、12米 D、15米

查看试题解析
10. 如图，在RtΔABC中，∠ACB=90，AC=6、BC=4，点F为射线CB上一动点，过点C作CM⊥AF于M交AB于E， D是AB的中点，则DM长度的最小值是（）

A、 $\sqrt{3}$ B、 $\sqrt{2}$ C、1 D、 $\sqrt{6}$ -2

查看试题解析

二、填空题

11. 二次函数 $y = x^{2} - 3$ 图象的顶点坐标为

查看试题解析
12. 如图，AB是⊙O的直径，弦CD⊥AB于点E，AB=4，CD=2 $\sqrt{2}$ ，则BE的长度是

查看试题解析
13. 已知点A是y= $\frac{k}{x}$ （x＞0）图象上的一点，点B是x轴负半轴上一点，连接AB，交y轴于点C，若AC=BC， S_△_BOC=1，则k的值是

查看试题解析
14. 如图，在△ABC中，AB=9、BC=6，∠ACB=2∠A，CD平分∠ACB交于AB点D，点M是AC一动点（AM＜ $\frac{1}{2}$ AC），将△ADM沿DM折叠得到△EDM，点A的对应点为点E，ED与AC交于点F，则CD的长度是；若ME//CD，则AM的长度是；

查看试题解析

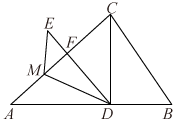
三、解答题

15. 计算：sin45°•cos45°-tan60°÷cos30°

查看试题解析
16. 如图，在由边长为1个单位长度的小正方形组成的网格中，给出了以格点(网格线的交点)为顶点的△ABC和格点O.

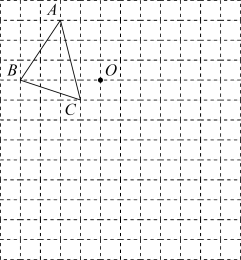
( 1 )以点O为位似中心，将△ABC放大2倍得到ΔA₁B₁C₁ ，在网格中画出ΔA₁B₁C₁；

( 2 )将△ABC绕点O逆时针旋转90°得ΔA₂B₂C₂ ，画出ΔA₂B₂C₂；

查看试题解析
17. 已知一次函数y₁=kx+b与反比例函数y₂= $\frac{6}{x}$ 的图像交于点A(3，m)、B(n，-3)；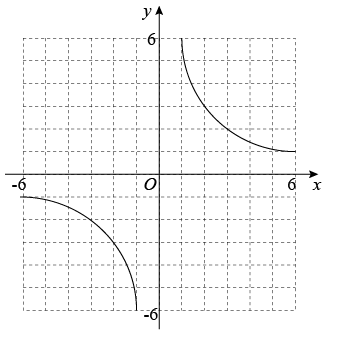

(1)、求一次函数的解析式；

(2)、在图中画出一次函数的图象，并根据图象直接写出y₁＞y₂的自变量x的取值范围．

查看试题解析
18. 已知，如图，AB//DC，∠ABC+∠ADB=180°.

(1)、求证：△ABD∽△BDC；

(2)、若AE平分∠DAB，BF平分∠DBC，且BF=2AE，S_△ABD=3，求S_△BDC

查看试题解析
19. 数学兴趣小组的成员在观察点A测得观察点B在A的正北方向，古树C在A的东北方向；在B处测得C在B的南偏东63.5°的方向上，古树D在B的北偏东53°的方向上，已知D在C正北方向上，即CD//AB，AC=50 $\sqrt{2}$ 米，求古树C、D之间的距离。(结果保留到0.1米，参考数据： $\sqrt{2}$ ≈1.41 ，sin63.5°≈0.89，cos63.5°≈0.45，tan63.5°≈2.00，sin53°≈0.80 ，cos53°≈0.60，tan53°≈1.32)

查看试题解析
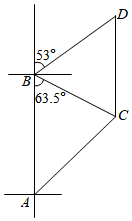20. 二次函数y=ax²+bx+4的部分对应值如表所示：
x
…
0
1
2
3
4
…
y=ax²+bx+4
…
4
6
6
4
0
…

(1)、求二次函数的解析式，并求其图象的对称轴；

(2)、点（m，y₁）、（2-m，y₂）是其图像上的两点，若m＞ $\frac{3}{2}$ ，则y₁y₂(填“＞”、“＜”或“=”)

查看试题解析
21. 如图，已知AB是⊙0的直径，C为⊙O上一点，∠OCB的平分线交⊙0于点D，过点D作⊙0的切线交CB的延长线于点E.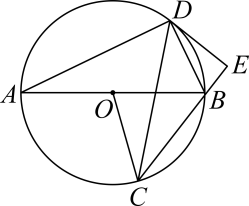

(1)、求证：CE⊥DE；

(2)、若AB=10， tanA= $\frac{1}{3}$ ，求DE的长.

查看试题解析
22. 已知如图，直线y=2x+4与x轴、y轴交于点A、B，抛物线y= $- \frac{1}{2}$ x²+bx+c经过点A、B，与x轴交于点C．

(1)、求b、c的值，并求直线BC的解析式；

(2)、点P是第一象限内抛物线上一动点，过点P作x轴的垂线，交直线AB、 BC于点M、N，连接CM，小明认为：当△CMN面积最大时，线段PN的长度最大，小明的想法对吗？请说明理由．

查看试题解析
23. 如图1，△ABC≌△DAE，∠BAC=∠ADE=90°。

(1)、连接CE，若AB=1，点B、C、E在同一条直线上，求AC的长；

(2)、将△ADE绕点A逆时针旋转α(0°＜α＜90°)，如图2，BC与AD交于点F，BC的延长线与AE交于点N，过点D，作 $D M / / A E$ 交BC于点M，求证：①BM=DM；②MN²=NF·NB.

查看试题解析

x	…	0	1	2	3	4	…
y=ax²+bx+4	…	4	6	6	4	0	…