安徽省滁州市凤阳县2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-10-09 类型:期末考试
一、单选题
-
1. 函数y=﹣2x2先向右平移1个单位,再向下平移2个单位,所得函数解析式是( )A、y=﹣2(x﹣1)2+2 B、y=﹣2(x﹣1)2﹣2 C、y=﹣2(x+1)2+2 D、y=﹣2(x+1)2﹣22. 在中, , 若 , , 则的长是( )A、80 B、 C、60 D、3. 如图,点P在的边上,若要判定 , 则下列添加的条件错误的是( )
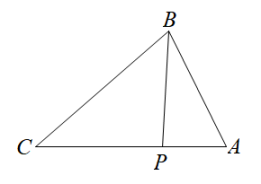 A、 B、 C、 D、4. 已知抛物线y=-(x+1)2上的两点A(x1 , y1)和B(x2 , y2),如果x1<x2<-1,那么下列结论一定成立的是( )A、 B、 C、 D、5. 如图, 、 是 上的两点, , 交 于点 ,则 等于( )
A、 B、 C、 D、4. 已知抛物线y=-(x+1)2上的两点A(x1 , y1)和B(x2 , y2),如果x1<x2<-1,那么下列结论一定成立的是( )A、 B、 C、 D、5. 如图, 、 是 上的两点, , 交 于点 ,则 等于( )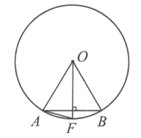 A、 B、 C、 D、6. 如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ADC的值为( )
A、 B、 C、 D、6. 如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ADC的值为( )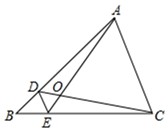 A、1:16 B、1:18 C、1:20 D、1:247. 下列语句中,正确的是( )A、任何一个圆都只有一个圆内接三角形 B、钝角三角形的外心在三角形内部 C、三角形的外心是到三角形三边的距离相等的交点 D、三角形的外心是三角形三边垂直平分线交点8. 如图,点A在双曲线上,点B在双曲线上,轴,交y轴于点C.若 , 则k的值为( )
A、1:16 B、1:18 C、1:20 D、1:247. 下列语句中,正确的是( )A、任何一个圆都只有一个圆内接三角形 B、钝角三角形的外心在三角形内部 C、三角形的外心是到三角形三边的距离相等的交点 D、三角形的外心是三角形三边垂直平分线交点8. 如图,点A在双曲线上,点B在双曲线上,轴,交y轴于点C.若 , 则k的值为( )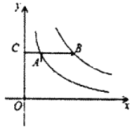 A、6 B、8 C、10 D、129. 如图,在⊙O中,AE是直径,半径OC垂直于弦AB于D,连接BE,若AB=2 ,CD=1,则BE的长是( )
A、6 B、8 C、10 D、129. 如图,在⊙O中,AE是直径,半径OC垂直于弦AB于D,连接BE,若AB=2 ,CD=1,则BE的长是( )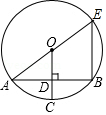 A、5 B、6 C、7 D、810. 如图,平行四边形ABCD中,对角线AC、BD相交于点O,且AC=6,BD=8,P是对角线BD上任意一点,过点P作EF∥AC,与平行四边形的两条边分别交于点E、F.设BP=x,EF=y,则能大致表示y与x之间关系的图象为( )
A、5 B、6 C、7 D、810. 如图,平行四边形ABCD中,对角线AC、BD相交于点O,且AC=6,BD=8,P是对角线BD上任意一点,过点P作EF∥AC,与平行四边形的两条边分别交于点E、F.设BP=x,EF=y,则能大致表示y与x之间关系的图象为( )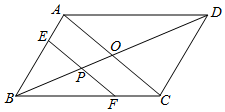 A、
A、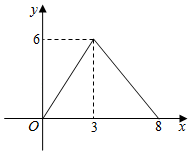 B、
B、 C、
C、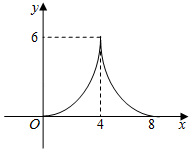 D、
D、
二、填空题
-
11. .
12. 抛物线y=2x2﹣4x+1的对称轴为直线 .13. 如图,半径为3的经过原点O和点 , 点B是y轴左侧优弧上一点,则为 .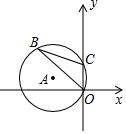 14. 在平面直角坐标系中,已知抛物线恰好经过和两点.(1)、求a的值;(2)、平移抛物线 , 使其顶点仍在直线上,求平移后所得抛物线与y轴交点纵坐标的最大值 .
14. 在平面直角坐标系中,已知抛物线恰好经过和两点.(1)、求a的值;(2)、平移抛物线 , 使其顶点仍在直线上,求平移后所得抛物线与y轴交点纵坐标的最大值 .三、解答题
-
15. 计算:.16. 已知线段a、b、c满足且 .(1)、求线段a、b、c的长;(2)、若线段x是线段a、b的比例中项(),求线段x的长.17. 如图,在平面直角坐标系中,点B的坐标为(3,﹣1).
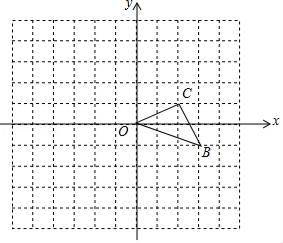 (1)、以点O为位似中心,在y轴的左侧将△OBC放大到原来的两倍(即新图与原图的相似比为2),画出放大后的△OB′C′;(2)、在(1)的基础上写出点B′,C′的坐标;(3)、在(1)的基础上,如果△OBC内部一点M的坐标为(a,b),请写出M的对应点M′的坐标.18. 为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山。汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶。已知BC=80千米,∠A=45°,∠B=30°。
(1)、以点O为位似中心,在y轴的左侧将△OBC放大到原来的两倍(即新图与原图的相似比为2),画出放大后的△OB′C′;(2)、在(1)的基础上写出点B′,C′的坐标;(3)、在(1)的基础上,如果△OBC内部一点M的坐标为(a,b),请写出M的对应点M′的坐标.18. 为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山。汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶。已知BC=80千米,∠A=45°,∠B=30°。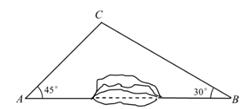 (1)、开通隧道前,汽车从A地到B地大约要走多少千米?(2)、开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据: ≈1.41, ≈1.73)19. 如图,直线 ( 为常数, 与双曲线 交于 , 两点,与 轴、 轴分别交于 , 两点,点 的坐标为 ,点 的坐标为 .
(1)、开通隧道前,汽车从A地到B地大约要走多少千米?(2)、开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据: ≈1.41, ≈1.73)19. 如图,直线 ( 为常数, 与双曲线 交于 , 两点,与 轴、 轴分别交于 , 两点,点 的坐标为 ,点 的坐标为 .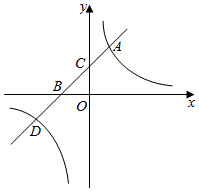 (1)、求直线的解析式.(2)、结合图象直接写出当 时, 的取值范围.20. 如图,为半圆O的直径,为切线,交半圆O于点D,点E为上一点,且 , 的延长线交于点F,连接 .
(1)、求直线的解析式.(2)、结合图象直接写出当 时, 的取值范围.20. 如图,为半圆O的直径,为切线,交半圆O于点D,点E为上一点,且 , 的延长线交于点F,连接 .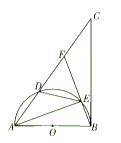 (1)、求证∶;(2)、若 , , 求的长.21. 如图, 与 交于点O, ,E为 延长线上一点,过点E作 ,交 的延长线于点F.
(1)、求证∶;(2)、若 , , 求的长.21. 如图, 与 交于点O, ,E为 延长线上一点,过点E作 ,交 的延长线于点F.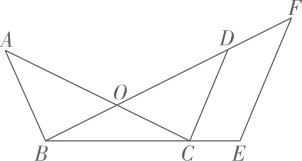 (1)、求证 ;(2)、若 ,求 的长.22. 某运动品牌销售商发现某种运动鞋市场需求量较大,经过市场调查发现月销售量y(双)与销售单价x(元)之间的函数关系为 , 而该种运动鞋的进价z(元)与销售单价x(元)之间的函数关系为 , 已知销售商每月支付员工工资和场地租金等费用总计20000元(注:月获利=月销售总额-月进货总价-工资和租金费用)(1)、求月获利W(元)与x之间的函数关系式;(2)、当销售单价x为何值时,月获利最大,最大值为多少?(3)、若该销售商销售这种品牌运动鞋的月获利不低于2.2万元,请确定销售单价的范围,在此情况下,要使销售量最大,你认为销售单价应定为多少元?23. 如图①,在正方形中,点E为边的中点,P为对角线上的一点,连接交于点F,连接、、 .
(1)、求证 ;(2)、若 ,求 的长.22. 某运动品牌销售商发现某种运动鞋市场需求量较大,经过市场调查发现月销售量y(双)与销售单价x(元)之间的函数关系为 , 而该种运动鞋的进价z(元)与销售单价x(元)之间的函数关系为 , 已知销售商每月支付员工工资和场地租金等费用总计20000元(注:月获利=月销售总额-月进货总价-工资和租金费用)(1)、求月获利W(元)与x之间的函数关系式;(2)、当销售单价x为何值时,月获利最大,最大值为多少?(3)、若该销售商销售这种品牌运动鞋的月获利不低于2.2万元,请确定销售单价的范围,在此情况下,要使销售量最大,你认为销售单价应定为多少元?23. 如图①,在正方形中,点E为边的中点,P为对角线上的一点,连接交于点F,连接、、 .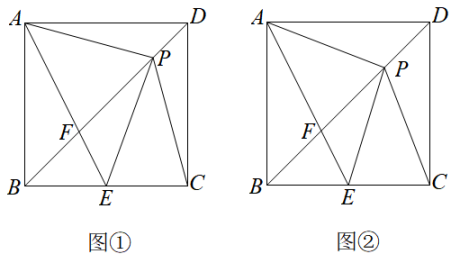 (1)、求证:;(2)、若 , 求证:;(3)、如图②,若 , , 求的长.
(1)、求证:;(2)、若 , 求证:;(3)、如图②,若 , , 求的长.