高中数学高三复习：平面向量与不等式章节检测练习

试卷更新日期：2022-10-09 类型：一轮复习

进入出卷网下载

一、单选题

1. 设 $x \in R$ ，则“ $\frac{x - 5}{x + 2} < 0$ ”是“ $| x - 2 | < 1$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分又不必要条件

查看试题解析
2. 设正实数m，n满足 $m + n = 2$ ，则 $\frac{n}{m} + \frac{1}{2 n}$ 的最小值是（）

A、 $\frac{3}{2}$ B、 $\frac{5}{2}$ C、 $\frac{5}{4}$ D、 $\frac{9}{4}$

查看试题解析
3. 已知 $| \vec{a} | = | \vec{b} | = 2$ ，且 $\vec{a}$ ， $\vec{b}$ 的夹角为 $6 0^{∘}$ ，若向量 $| \vec{c} - \vec{a} | \leq 1$ ，则 $\vec{b} \cdot \vec{c}$ 的取值范围是（）

A、 $[- 4 ， 4]$ B、 $[- 2 \sqrt{3} ， 2 \sqrt{3}]$ C、 $[0 ， 2 \sqrt{3}]$ D、 $[0 ， 4]$

查看试题解析
4. 已知 $\vec{a}$ ， $\vec{b}$ 是平面内两个不共线的向量， $\vec{A B} = \vec{a} + λ \vec{b}$ ， $\vec{A C} = μ \vec{a} + \vec{b}$ ， $λ$ ， $μ \in R$ ，则 $A$ ， $B$ ， $C$ 三点共线的充要条件是（）

A、 $λ - μ = 1$ B、 $λ + μ = 2$ C、 $λ μ = 1$ D、 $\frac{λ}{μ} = 1$

查看试题解析
5. 在 $△ A B C$ 中，M为BC边上任意一点，N为线段AM上任意一点，若 $\vec{A N} = λ \vec{A B} + μ \vec{A C}$ （ $λ$ ， $μ \in R$ ），则 $λ + μ$ 的取值范围是（）

A、 $[0 ， \frac{1}{3}]$ B、 $[\frac{1}{3} ， \frac{1}{2}]$ C、 $[0 ， 1]$ D、 $[1 ， 2]$

查看试题解析
6. 如图在 $△ A B C$ 中， $∠ A B C = 90 °$ ， $F$ 为 $A B$ 中点， $C E = 3$ ， $C B = 8$ ， $A B = 12$ ，则 $\vec{E A} \cdot \vec{E B} =$ （）

A、-15 B、-13 C、13 D、14

查看试题解析
7. 已知 $4 x^{4} + 9 x^{2} y^{2} + 2 y^{4} = 1$ ，则 $5 x^{2} + 3 y^{2}$ 的最小值是（）

A、2 B、 $\frac{12}{7}$ C、 $\frac{5}{2}$ D、3

查看试题解析
8. 已知△ABC中， $A B = 4$ ， $A C = 3$ ， $c o s A = \frac{1}{3}$ ．若D为边BC上的动点，则 $\vec{A B} \cdot \vec{A D}$ 的取值范围是（）

A、 $[4 \sqrt{2} ， 12]$ B、 $[8 \sqrt{2} ， 16]$ C、 $[4 ， 16]$ D、 $[2 ， 4]$

查看试题解析

二、多选题

9. 八卦是我国古代的一套有象征意义的符号.如图1是八卦模型图，其平面图形记为图2中的正八边形ABCDEFGH，其中 $| O A | = 1$ ，则（）

A、 $\vec{E F} = \vec{A B}$ B、 $\vec{O B} + \vec{O H} = - \sqrt{2} \vec{O E}$ C、 $\vec{O A} \cdot \vec{O D} = - \frac{\sqrt{2}}{2}$ D、 $\vec{A H} \cdot \vec{H O} = \vec{B C} \cdot \vec{B O}$

查看试题解析
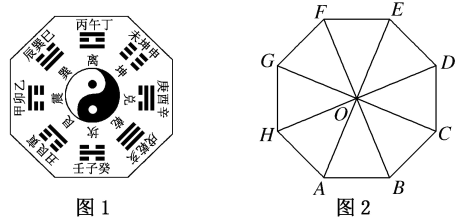10. 下列说法正确的是（）

A、命题“ $\forall x > 0$ ，都有 $e^{x} > x + 1$ ”的否定是“ $\exists x \leq 0$ ，使得 $e^{x} \leq x + 1$ ” B、当 $x > 1$ 时， $x + \frac{4}{x - 1}$ 的最小值是5 C、若不等式 $a x^{2} + 2 x + c > 0$ 的解集为 ${x | - 1 < x < 2}$ ，则 $a + c = 2$ D、“ $a > 1$ ”是“ $\frac{1}{a} < 1$ ”的充要条件

查看试题解析
11. 已知x>0，y>0，且x+2y=3，则下列正确的是（）

A、 $\frac{1}{x} + \frac{2}{y}$ 的最小值为3 B、 $\sqrt{x} + \sqrt{2 y}$ 的最大值为6 C、xy的最大值为 $\frac{9}{8}$ D、 $2^{x + 1} + 4^{y} \geq 8$

查看试题解析
12. 已知非零向量 $\vec{a}$ ， $\vec{b}$ 的夹角为 $θ$ ，现定义一种新运算： $\vec{a} \otimes \vec{b} = | \vec{a} | | \vec{b} | s i n θ$ ．若 $\vec{a} = (x_{1} ， y_{1})$ ， $\vec{b} = (x_{2} ， y_{2})$ ， $\vec{c} = (x_{3} ， y_{3})$ ，则（）

A、 $\vec{a}$ 在 $\vec{b}$ 上的投影向量的模为 $\frac{\vec{a} \otimes \vec{b}}{| \vec{a} |}$ B、 $\exists θ \in [0 ， \frac{π}{2}]$ ， $\vec{a} \otimes \vec{b} = \vec{a} \cdot \vec{b}$ C、 $\vec{a} \otimes \vec{b} = |x_{1} y_{2} - x_{2} y_{1}|$ D、 $\vec{a} \otimes (\vec{b} - \vec{c}) = \vec{a} \otimes \vec{b} - \vec{a} \otimes \vec{c}$

查看试题解析

三、填空题

13. 若 $a > 2 ， b > - 1$ ，且满足 $a b + a - 2 b = 6$ ，则 $\frac{1}{a - 2} + \frac{9}{b + 1}$ 的最小值为．

查看试题解析
14. 已知向量 $\vec{a} = (λ ， 1)$ ， $\vec{b} = (2 ， - 3)$ ，若 $(\vec{a} - \vec{b}) ⊥ \vec{b}$ ，则 $λ =$ ．

查看试题解析
15. 如图，在 $△ A B C$ 中， $∠ B A C = \frac{π}{3}$ ， $\vec{A D} = \frac{2}{3} \vec{A B}$ ，点P在线段CD上（P不与C，D点重合），若 $△ A B C$ 的面积为 $4 \sqrt{3}$ ， $\vec{A P} = m \vec{A C} + \frac{1}{2} \vec{A B}$ ，则实数m＝， $| \vec{A P} |$ 的最小值为．

查看试题解析
16. 已知半径为1的圆O上有三个动点A，B，C，且 $| A B | = \sqrt{2}$ ，则 $\vec{A C} \cdot \vec{B C}$ 的最小值为．

查看试题解析

四、解答题

17. 已知 $\vec{a} = (1 ， 2)$ ， $\vec{b} = (- 3 ， 1)$

(1)、设 $\vec{a}$ ， $\vec{b}$ 的夹角为 $θ$ ，求 $s i n θ$ 的值；

(2)、若向量 $\vec{a} + k \vec{b}$ 与 $\vec{a} - k \vec{b}$ 共线，求 $k$ 的值．

查看试题解析
18. 已知单位向量 $\vec{e_{1}}$ ， $\vec{e_{2}}$ 的夹角为 $\frac{π}{3}$ ，且向量 $\vec{a} = 2 \vec{e_{1}} - \vec{e_{2}}$ ， $\vec{b} = - \vec{e_{1}} + 3 \vec{e_{2}}$ ．

(1)、用 $\vec{e_{1}}$ ， $\vec{e_{2}}$ 表示出一个与 $2 \vec{a} + \vec{b}$ 共线的非零向量；

(2)、求 $\vec{a}$ 与 $\vec{b}$ 夹角的余弦值．

查看试题解析
19. 已知函数 $f (x) = \sqrt{3} s i n x c o s x - \frac{1}{2} c o s 2 x - 1$ ， $x \in R$ .

(1)、求函数 $f (x)$ 的最小值和最小正周期；

(2)、已知 $△ A B C$ 内角A，B，C的对边分别为a，b，c，且 $c = 3$ ， $f (C) = 0$ ，若向量 $\vec{m} = (1 ， s i n A)$ 与 $\vec{n} = (2 ， s i n B)$ 共线，求a，b的值.

查看试题解析
20. 记 $△ A B C$ 的内角A，B，C的对边分别为a，b，c，满足 $(t a n A - s i n C) (t a n B - s i n C) = s i n^{2} C$ ．

(1)、求证： $c^{2} = a b$ ；

(2)、若 $a + b = 3$ ，求 $\vec{C A} \cdot \vec{C B}$ 的最小值．

查看试题解析
21. 已知函数 $f (x) = x^{2} - x + m$ ．

(1)、当 $m = - 6$ 时，解不等式 $f (x) > 0$ ；

(2)、当 $m > 0$ 时， $f (x) < 0$ 的解集为 $(a ， b)$ ，求 $\frac{a + 1}{a} + \frac{4}{b}$ 的最小值．

查看试题解析
22. 如图，扇形 $O P Q$ 区域（含边界）是一风景旅游区，其中P，Q分别在公路OA和OB上．经测得，扇形 $O P Q$ 区域的圆心角 $∠ P O Q = \frac{π}{3}$ ，半径为5千米．为了方便旅游参观，打算在扇形 $O P Q$ 区域外修建一条公路 $M N$ ，分别与OA和OB交于M，N两点，并且MN与 $\overset{⌢}{P Q}$ 相切于点S（异于点P，Q），设 $∠ P O S = α$ （弧度），将公路 $M N$ 的长度记为 $y$ （单位：千米），假设所有公路的宽度均忽略不计．

(1)、将y表示为 $α$ 的函数，并写出 $α$ 的取值范围；

(2)、求y的最小值，并求此时 $α$ 的值．

查看试题解析