2022年秋季浙教版数学九年级上册第三章《 圆的基本性质》单元测试A
试卷更新日期:2022-10-09 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 如图,已知△ABC中,∠CAB=20°,∠ABC=30°,将△ABC绕A点逆时针旋转50°得到△AB′C′,以下结论:①BC=B′C′,②AC∥C′B′,③C′B′⊥BB′,④∠ABB′=∠ACC′,正确的有( )
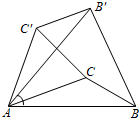 A、①②③ B、①②④ C、①③④ D、②③④2. 如图, 内接于 ,CD是 的直径, ,则 ( )
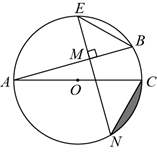
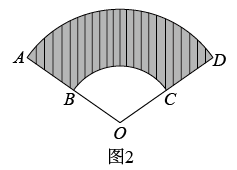
A、①②③ B、①②④ C、①③④ D、②③④2. 如图, 内接于 ,CD是 的直径, ,则 ( )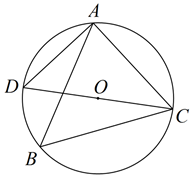 A、70° B、60° C、50° D、40°3. 如图1是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角 形成的扇面,若 , ,则阴影部分的面积为( )
A、70° B、60° C、50° D、40°3. 如图1是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角 形成的扇面,若 , ,则阴影部分的面积为( )
 A、 B、 C、 D、4. 如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则 的长为( )
A、 B、 C、 D、4. 如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则 的长为( )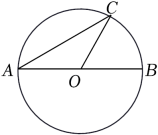 A、6π B、2π C、π D、π5. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )
A、6π B、2π C、π D、π5. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )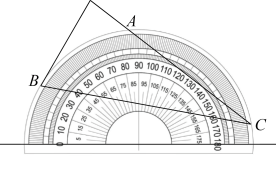 A、28° B、30° C、36° D、56°6. 如图,在Rt△ABC中, , , , 将绕点B顺时针旋转90°得到.在此旋转过程中所扫过的面积为( )
A、28° B、30° C、36° D、56°6. 如图,在Rt△ABC中, , , , 将绕点B顺时针旋转90°得到.在此旋转过程中所扫过的面积为( ) A、25π+24 B、5π+24 C、25π D、5π7. 如图,AB是⊙O的直径,PA与⊙O相切于点A,∠ABC=25°,OC的延长线交PA于点P,则∠P的度数是( )
A、25π+24 B、5π+24 C、25π D、5π7. 如图,AB是⊙O的直径,PA与⊙O相切于点A,∠ABC=25°,OC的延长线交PA于点P,则∠P的度数是( )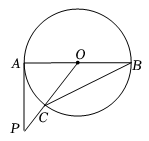 A、25° B、35° C、40° D、50°8. 下列说法错误的是( )A、对角线垂直且互相平分的四边形是菱形 B、同圆或等圆中,同弧对应的圆周角相等 C、对角线相等的四边形是矩形 D、对角线垂直且相等的平行四边形是正方形9. 如图,AB,CD是的弦,延长AB,CD相交于点P.已知 , , 则的度数是( )
A、25° B、35° C、40° D、50°8. 下列说法错误的是( )A、对角线垂直且互相平分的四边形是菱形 B、同圆或等圆中,同弧对应的圆周角相等 C、对角线相等的四边形是矩形 D、对角线垂直且相等的平行四边形是正方形9. 如图,AB,CD是的弦,延长AB,CD相交于点P.已知 , , 则的度数是( )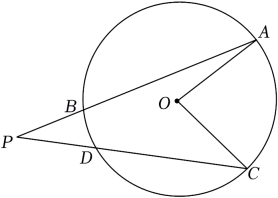 A、30° B、25° C、20° D、10°10. 如图,四边形是的内接四边形.若 , 则的度数为( )
A、30° B、25° C、20° D、10°10. 如图,四边形是的内接四边形.若 , 则的度数为( )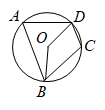 A、138° B、121° C、118° D、112°
A、138° B、121° C、118° D、112°二、填空题(每题3分,共18分)
-
11. 如图,点A,B,C在 上, ,则 度.
 12. 如图,四边形ABCD内接于⊙O,AB为⊙O的直径,∠ADC=130°,连接AC,则∠BAC的度数为 .
12. 如图,四边形ABCD内接于⊙O,AB为⊙O的直径,∠ADC=130°,连接AC,则∠BAC的度数为 .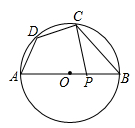 13. 如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,如果C是中弦AB的中点,CD经过圆心O交于点D,并且 , , 则的半径长为m.
13. 如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,如果C是中弦AB的中点,CD经过圆心O交于点D,并且 , , 则的半径长为m. 14. 如图,A、B、C是上的点, , 垂足为点D,且D为OC的中点,若 , 则BC的长为.
14. 如图,A、B、C是上的点, , 垂足为点D,且D为OC的中点,若 , 则BC的长为. 15. 如图,等边三角形ABC内接于⊙O,BC=2 , 则图中阴影部分的面积是 .
15. 如图,等边三角形ABC内接于⊙O,BC=2 , 则图中阴影部分的面积是 .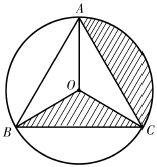 16. 如图,在△ABC中,AB=AC,点O在边AC上,以O为圆心,4为半径的圆恰好过点C,且与边AB相切于点D,交BC于点E,则劣弧的长是(结果保留)
16. 如图,在△ABC中,AB=AC,点O在边AC上,以O为圆心,4为半径的圆恰好过点C,且与边AB相切于点D,交BC于点E,则劣弧的长是(结果保留)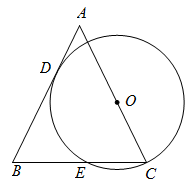
三、解答题(共8题,共72分)
-
17. 证明:垂直于弦的直径平分弦以及弦所对的两条弧.
 18. 如图,△ABC内接于⊙O,交⊙O于点D,交BC于点E,交⊙O于点F,连接AF,CF.
18. 如图,△ABC内接于⊙O,交⊙O于点D,交BC于点E,交⊙O于点F,连接AF,CF.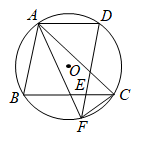 (1)、求证:AC=AF;(2)、若⊙O的半径为3,∠CAF=30°,求的长(结果保留π).19. 如图,C,D是以AB为直径的半圆上的两点, , 连结BC,CD.
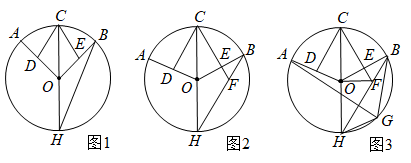
(1)、求证:AC=AF;(2)、若⊙O的半径为3,∠CAF=30°,求的长(结果保留π).19. 如图,C,D是以AB为直径的半圆上的两点, , 连结BC,CD. (1)、求证: .(2)、若 , , 求阴影部分的面积.20. 如图,已知在⊙O中, ,OC与AD相交于点E.求证:
(1)、求证: .(2)、若 , , 求阴影部分的面积.20. 如图,已知在⊙O中, ,OC与AD相交于点E.求证: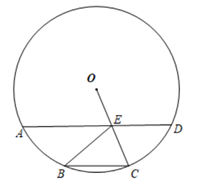 (1)、AD∥BC(2)、四边形BCDE为菱形.21. 如图,已知AB是⊙O的直径,∠ACD是 所对的圆周角,∠ACD=30°。
(1)、AD∥BC(2)、四边形BCDE为菱形.21. 如图,已知AB是⊙O的直径,∠ACD是 所对的圆周角,∠ACD=30°。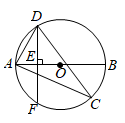 (1)、求∠DAB的度数;(2)、过点D作DE⊥AB,垂足为E,DE的延长线交⊙O于点F。若AB=4,求DF的长。22. 如图,△ABC内接于⊙O,AB为⊙O的直径,AB=10,AC=6。连结OC,弦AD分别交OC,BC于点E,F,其中点E是AD的中点。
(1)、求∠DAB的度数;(2)、过点D作DE⊥AB,垂足为E,DE的延长线交⊙O于点F。若AB=4,求DF的长。22. 如图,△ABC内接于⊙O,AB为⊙O的直径,AB=10,AC=6。连结OC,弦AD分别交OC,BC于点E,F,其中点E是AD的中点。 (1)、求证:∠CAD=∠CBA。(2)、求OE的长。
(1)、求证:∠CAD=∠CBA。(2)、求OE的长。