人教版七上数学第四章4.3.3余角和补角 课时易错题三刷(第三刷)
试卷更新日期:2022-10-08 类型:同步测试
一、单选题
-
1. 如图,货轮在O处观测到岛屿B在北偏东45°的方向,岛屿C在南偏东60°的方向,则∠BOC的大小是( )
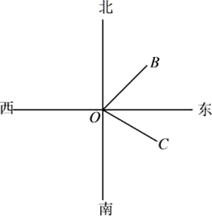 A、75° B、80° C、100° D、105°2. 如图,甲从A处出发沿北偏东60°方向走向B处,乙从A处出发沿南偏西30°方向走到C处,则∠BAC的度数是 ( )
A、75° B、80° C、100° D、105°2. 如图,甲从A处出发沿北偏东60°方向走向B处,乙从A处出发沿南偏西30°方向走到C处,则∠BAC的度数是 ( )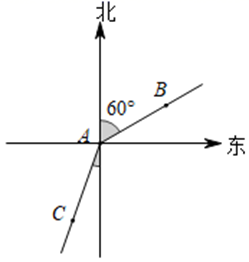 A、 B、 C、 D、3. 如果一个角的补角是这个角的4倍,那么这个角为( )A、36° B、30° C、144° D、150°4. 若与互为余角,与互为补角,则下列结论:①;②;③;④ . 其中正确的有( )A、4个 B、3个 C、2个 D、1个
A、 B、 C、 D、3. 如果一个角的补角是这个角的4倍,那么这个角为( )A、36° B、30° C、144° D、150°4. 若与互为余角,与互为补角,则下列结论:①;②;③;④ . 其中正确的有( )A、4个 B、3个 C、2个 D、1个二、填空题
-
5. 已知∠A的补角是142°,则∠A的余角的度数是.6. 如果一个角余角的度数为42°51′,那么这个角补角的度数.7. 将两块直角三角尺的直角顶点重合为如图的位置,若∠AOC=20°,则∠BOD= .
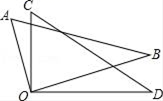 8. 若一个角的补角与这个角的余角之和为190°,则这个角的度数为度.9. 若与互余,且 , 则 .
8. 若一个角的补角与这个角的余角之和为190°,则这个角的度数为度.9. 若与互余,且 , 则 .三、综合题
-
10. 如图,直线AB与CD相交于点O,OE 是∠COB的平分线,OE⊥OF.
 (1)、图中∠BOE的补角是;(2)、若∠COF=2∠COE,求△BOE 的度数;(3)、试判断 OF是否平分∠AOC,请说明理由.11. 如图①,将一副常规直角三角尺的直角顶点叠放在一起, , . 解答下列问题.
(1)、图中∠BOE的补角是;(2)、若∠COF=2∠COE,求△BOE 的度数;(3)、试判断 OF是否平分∠AOC,请说明理由.11. 如图①,将一副常规直角三角尺的直角顶点叠放在一起, , . 解答下列问题.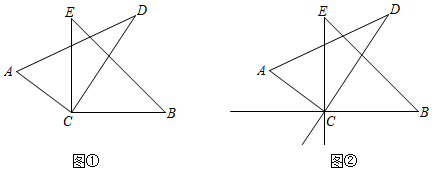 (1)、若∠DCE=35°24',则∠ACB=;若∠ACB=115°,则∠DCE=;(2)、当∠DCE=α时,求∠ACB的度数,并直接写出∠DCE与∠ACB的关系;(3)、在图①的基础上作射线BC,射线EC,射线DC,如图②,则与∠ECB互补的角有个.12. 已知:锐角∠AOB.(1)、若∠AOB=65°,则∠AOB的余角的度数为度.(2)、若∠AOB=53°17ʹ,则∠AOB的补角的度数为 .(3)、若∠AOB=31°12ʹ,计算:∠AOB= .(4)、若∠AOB=20°21ʹ,计算:3∠AOB.13. 已知 与 互补,射线 平分 ,设 , .
(1)、若∠DCE=35°24',则∠ACB=;若∠ACB=115°,则∠DCE=;(2)、当∠DCE=α时,求∠ACB的度数,并直接写出∠DCE与∠ACB的关系;(3)、在图①的基础上作射线BC,射线EC,射线DC,如图②,则与∠ECB互补的角有个.12. 已知:锐角∠AOB.(1)、若∠AOB=65°,则∠AOB的余角的度数为度.(2)、若∠AOB=53°17ʹ,则∠AOB的补角的度数为 .(3)、若∠AOB=31°12ʹ,计算:∠AOB= .(4)、若∠AOB=20°21ʹ,计算:3∠AOB.13. 已知 与 互补,射线 平分 ,设 , .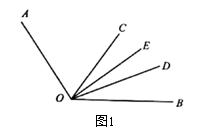
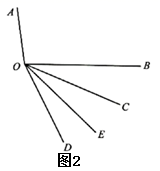 (1)、如图1, 在 的内部,
(1)、如图1, 在 的内部,①当 时,求 的值.
②当 时,求 的度数.
(2)、如图2, 在 的外部, ,求 与 满足的等量关系.14. 数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事休”.数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来从而实现优化解题途径的目的.请你利用“数形结合”的思想解决以下的问题: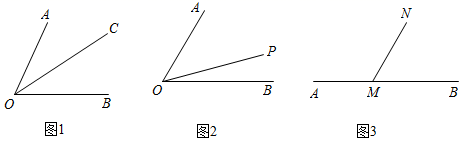 (1)、如图1:射线 是 的平分线,这时有数量关系: .(2)、如图2: 被射线 分成了两部分,这时有数量关系: .(3)、如图3:直线 上有一点 ,射线 从射线 开始绕着点 顺时针旋转,直到与射线 重合才停止.
(1)、如图1:射线 是 的平分线,这时有数量关系: .(2)、如图2: 被射线 分成了两部分,这时有数量关系: .(3)、如图3:直线 上有一点 ,射线 从射线 开始绕着点 顺时针旋转,直到与射线 重合才停止.①请直接回答 与 是如何变化的?
② 与 之间有什么关系?请说明理由.
15. 如图,直线 与 相交于点 , , , , 平分 . (1)、求 的度数;(2)、求 的度数.16. 如图1,直线DE上有一点O,过点O在直线DE上方作射线OC,将一直角三角板AOB(其中∠OAB=30°)的直角顶点放在点O处,一条直角边OA在射线OD上,另一边OB在直线DE上方,将直角三角板绕着点O按每秒10°的速度逆时针旋转一周,设旋转时间为t秒.
(1)、求 的度数;(2)、求 的度数.16. 如图1,直线DE上有一点O,过点O在直线DE上方作射线OC,将一直角三角板AOB(其中∠OAB=30°)的直角顶点放在点O处,一条直角边OA在射线OD上,另一边OB在直线DE上方,将直角三角板绕着点O按每秒10°的速度逆时针旋转一周,设旋转时间为t秒. (1)、当直角三角板旋转到如图2的位置时,OA恰好平分∠COD,此时,∠BOC与∠BOE之间有何数量关系 ;(2)、若射线OC的位值保持不变,且∠COE=140°
(1)、当直角三角板旋转到如图2的位置时,OA恰好平分∠COD,此时,∠BOC与∠BOE之间有何数量关系 ;(2)、若射线OC的位值保持不变,且∠COE=140°①在旋转的过程中,是否存在某个时刻,使得射线OA,OC,OD中的某一条射线是另两条射线所夹角的角平分线?若存在,请直接写出所有满足题意t的取值 ,若不存在,请说明理由;
②在旋转的过程中,当边AB与射线OE相交时,如图3,请直接写出∠AOC﹣∠BOE的值 .
17. 如图1,直线AB上任取一点O,过点O作射线OC(点C在直线AB上方),且∠BOC=2∠AOC,以O为顶点作∠MON=90°,点M在射线OB上,点N在直线AB下方,点D是射线ON反向延长线上的一点. (1)、求∠COD的度数;(2)、如图2,将∠MON绕点O逆时针旋转α度(0°<α<180°),若三条射线OD、OC、OA,当其中一条射线与另外两条射线所夹角的度数之比为1:2时,求∠BON的度数.18. 如图①,已知:射线OC⊥AB,垂足为O,∠DOE=90°,OM平分∠BOD.
(1)、求∠COD的度数;(2)、如图2,将∠MON绕点O逆时针旋转α度(0°<α<180°),若三条射线OD、OC、OA,当其中一条射线与另外两条射线所夹角的度数之比为1:2时,求∠BON的度数.18. 如图①,已知:射线OC⊥AB,垂足为O,∠DOE=90°,OM平分∠BOD.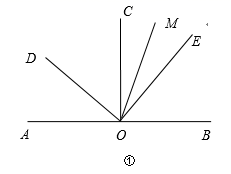
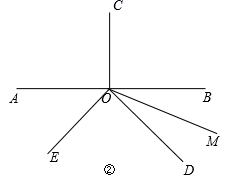 (1)、∠BOE与∠COD的关系是 , 理由是:;(2)、探索∠AOD与∠COM的关系,并说明理由;(3)、如图②,在上述条件下,将∠DOE旋转至直线AB的下方,请继续探索∠AOD与∠COM的关系,并说明理由.
(1)、∠BOE与∠COD的关系是 , 理由是:;(2)、探索∠AOD与∠COM的关系,并说明理由;(3)、如图②,在上述条件下,将∠DOE旋转至直线AB的下方,请继续探索∠AOD与∠COM的关系,并说明理由.