人教版七上数学第四章4.3.2角的比较与运算 课时易错题三刷（第三刷）
试卷更新日期：2022-10-08 类型：同步测试
一、单选题
-
1. 如图，OB是∠AOC的平分线，∠COD＝∠BOD，∠COD＝17°，则∠AOD的度数是（ ）
A、70° B、83° C、68° D、85°2. 如图，∠AOB，以OA为边作∠AOC，使∠BOC= ∠AOB，则下列结论成立的是（ ）
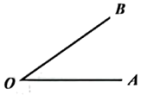A、 B、 C、 或 D、 或二、填空题
-
3. 如图，若∠AOB＝90°，∠COD＝90°，∠AOD＝20°，则∠BOC的大小为 °．
4. 如图，已知OD平分∠AOC，OE平分∠COB，∠AOD＝20°，∠EOB＝40°.则∠AOB＝.
5. 如图，将一个三角板60°角的顶点与另一个三角板的直角顶点重合，∠1＝27°41′，∠2的大小是 .
6. 如图，在∠AOB的内部有3条射线OC、OD、OE，若∠AOC＝70°，∠BOE＝ ∠BOC，∠BOD＝ ∠AOB，则∠DOE＝°.（用含n的代数式表示）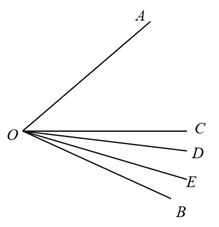
三、解答题
-
7. 补全解题过程．
已知：如图，∠AOB＝40°，∠BOC＝70°，OD平分∠AOC．
求∠BOD的度数．
解：∵∠AOB＝40°，∠BOC＝70°，
∴∠AOC＝∠AOB＋∠BOC＝ ▲ °．
∵OD平分∠AOC，
∴∠AOD＝∠ ▲ （ ▲ ）（填写推理依据）．
∴∠AOD＝ ▲ °．
∴∠BOD＝∠AOD﹣∠ ▲ ．
∴∠BOD＝ ▲ °．
8. 完成下列说理过程（括号中填写推理的依据）：已知：如图，直线AB，CD相交于点O， ． 求证： ．
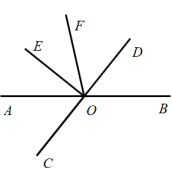
证明： ，
． （ ▲ ）
，
．
直线AB，CD相交于点O，
．
．
＝ ▲ ． （ ▲ ）
直线相交于 ，
．
▲ ． （ ▲ ）
．
9. 如图，已知 平分 ，∠COD=20°，求 的度数.
四、综合题
-
10. 如图，点O是直线AB上的一点，∠COD是直角，OE平分∠BOC．
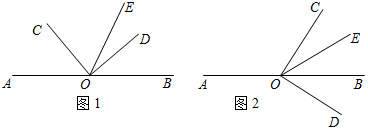(1)、如图（1），若∠AOC=40°，求∠DOE的度数；(2)、如图（2），若∠COE=∠DOB，求∠AOC的度数．11. 如图1，将一副三角尺的直角顶点O叠放在一起.若三角尺AOB不动，将三角尺COD绕点O按顺时针方向转动α（0°<α<180°）.
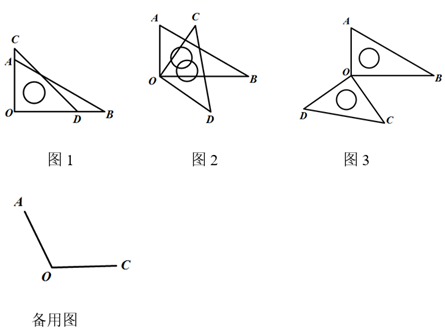(1)、如图2，若∠BOC=55°，则∠AOD= ， ∠AOC∠BOD（填“>”、“<”或“=”）；(2)、如图3，∠BOC=55°，则∠AOD= ， ∠AOC∠BOD（填“>”、“<”或“=”）.(3)、三角尺COD在转动的过程中，若∠BOC=β，则∠AOD=（用含β的代数式表示），∠AOC∠BOD（填“>”、“<”或“=”）.(4)、借助（3）中的结论，在备用图中利用画直角的工具画出一个与∠AOC相等的角.12. 已知：∠AOB=120°，∠COD=90°，OE平分∠AOD．
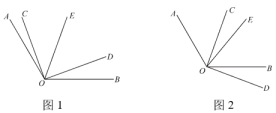(1)、如图1，当∠COD的边OD在∠AOB内部时，若∠COE=40°，求∠BOD的度数；(2)、如图2，当∠COD的边OD在∠AOB外部，且0°<∠BOD<60°时，设∠COE=α，∠BOD=β，用等式表示α与β之间的数量关系，并证明．13. 阅读下面材料：数学课上，老师给出了如下问题：
如图1，∠AOB＝80°，OC平分∠AOB，若∠BOD＝20°，请你补全图形，并求∠COD的度数.
以下是小明的解答过程：
解：如图2，因为OC平分∠AOB，∠AOB＝80°，
所以∠BOC＝_____∠AOB＝_____°
因为∠BOD＝20°，
所以∠COD＝______°
小静说：“我觉得这个题有两种情况，小明考虑的是OD在∠AOB外部的情况，事实上，OD还可能在∠AOB的内部”.
完成以下问题：
(1)、请你将小明的解答过程补充完整；(2)、根据小静的想法，请你在图3中画出另一种情况对应的图形，并直接写出此时∠COD的度数为▲ °14. 已知射线OB，OC在钝角的内部，且满足 ， 射线OE，OF分别平分 ．
(1)、如图1，当射线OC在射线OB的左侧时， ，①若 ， ▲ ；
②若 ， ▲ ；
③若 ， 计算的度数．
(2)、当射线OC在射线OB的右侧时，设 ， 请画出图形并计算的度数（用含的式子表示）．
