人教版七上数学第四章4.3.2角的比较与运算 课时易错题三刷（第二刷）

试卷更新日期：2022-10-08 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 关于角的描述不正确的是（  ）

    A、∠1与∠AOB表示同一个角 B、∠AOC可以用∠O表示 C、∠AOC＝∠AOB+∠BOC D、∠β表示∠BOC

    查看试题解析

  • 2. 将一副三角板如图①的位置摆放，其中30°直角三角板的直角边与等腰直角三角板的斜边重合，30°直角三角板直角顶点与等腰直角三角板的锐角顶点重合（为点O）．现将30°的直角三角板绕点O顺时针旋转至如图②的位置，此时∠1为25°，则∠2=（      ）

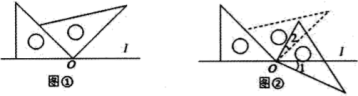    A、15° B、20° C、25° D、30°

    查看试题解析

  • 3. 如图，将一副直角三角板叠放在一起，使直角顶点重合于点O，则∠COB+∠AOD=（        ）

    A、135° B、150° C、180° D、360°

    查看试题解析

  • 4. 如图，将三个相同的正方形的一个顶点重合放置， ∠BAC=30° ， ∠DAE=35° ，那么 ∠1 的度数为（   ）

    A、20° B、25° C、30° D、35°

    查看试题解析

二、填空题

  • 5. 如图所示，点O是直线AB上一点，∠BOC＝130°，OD平分∠AOC．求∠COD的度数．

    解：∵点O是直线AB上一点，

    ∴∠AOB＝ ．

    ∵∠BOC＝130°，

    ∴∠AOC＝∠AOB－∠BOC＝

    ∵OD平分∠AOC，

    ∴∠COD＝12＝

    查看试题解析

  • 6. 如图，将一副三角尺的直角顶点O重合在一起．若∠COB与∠DOA的比是2：7，OP平分∠DOA，则∠POC＝度．

    查看试题解析

三、解答题

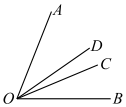
  • 7. 如图，∠AOC与∠BOC的度数比为5：2，OD平分∠AOB，若∠COD＝15°，求∠AOB的度数.

    查看试题解析

四、综合题

  • 8. 如图1，将一副直角三角板的两顶点重合叠放于点 O ，其中一个三角板的顶点 C 落在另一个三角板的边 OA 上.已知 ∠ABO=∠DCO=90∘ ， ∠AOB=45∘ ， ∠COD=60∘ ，作 ∠AOD 的平分线交边 CD 于点 E .

    (1)、求 ∠BOE 的度数；
    (2)、如图2，若点 C 不落在边 OA 上，当 ∠COE=15∘ 时，求 ∠BOD 的度数.

    查看试题解析

  • 9. 点O是直线AB上的一点，CO⊥DO ， OE平分∠BOC ．
    (1)、如图，若∠AOC=50° ， 求∠DOE的度数．

    (2)、如图，若∠COE=13∠DOB ， 求∠AOC的度数．

    查看试题解析

  • 10. 已知∠AOB＝90°，

    (1)、如图1，OE、OD分别平分∠AOB和∠BOC，若∠EOD＝64°，则∠BOC是°；
    (2)、如图2，OE、OD分别平分∠AOC和∠BOC，若∠BOC＝40°，求∠EOD的度数（写推理过程）．
    (3)、若OE、OD分别平分∠AOC和∠BOC，∠BOC＝α（0°＜α＜180°），则∠EOD的度数是（在稿纸上画图分析，直接填空）．

    查看试题解析

  • 11. 如图，OB是∠AOC的平分线，OD是∠COE的平分线．

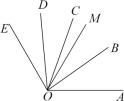    (1)、如果∠AOC＝70°，∠COE＝50°，求∠BOD的度数；
    (2)、如果∠AOE＝160°，求∠BOD的度数；
    (3)、如果OM平分∠AOE，∠COD：∠BOC＝2：3，∠COM＝15°，求∠BOD的度数．

    查看试题解析

  • 12. 如图，在桌上放置一副三角板（忽略厚度），直角(∠DAE)与60°角(∠BAC)顶点重合．三角板ADE可绕着点A旋转．

    (1)、当AD平分∠BAC时，求∠1的度数．
    (2)、在旋转过程中，保持AD在∠BAC内部，求∠1−∠2的度数．

    查看试题解析

  • 13. 如图，将一副直角三角板的直角顶点C叠放在一起.

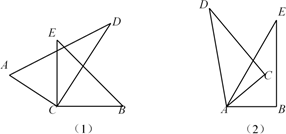    (1)、如图（1），若∠DCE＝33°，则∠BCD＝ ， ∠ACB＝.
    (2)、如图（1），猜想∠ACB与∠DCE的大小有何特殊关系？并说明理由.
    (3)、如图（2），若是两个同样的直角三角板60°锐角的顶点A重合在一起，则∠DAB与∠CAE的数量关系为.

    查看试题解析

  • 14. （问题回顾）

    我们曾解决过这样的问题：如图1，点O在直线 AB 上， OC ， OD 分别平分 ∠AOE ， ∠BOE ，可求得 ∠COD=90° .（不用求解）

    （问题改编）

    点O在直线 AB 上， ∠COD=90° ，OE平分 ∠BOC .

    (1)、如图2，若 ∠AOC=50° ，求 ∠DOE 的度数；
    (2)、将图2中的 ∠COD 按图3所示的位置进行放置，写出 ∠AOC 与 ∠DOE 度数间的等量关系，并写明理由.

    查看试题解析

  • 15. 如图1，点 D 、 O 、 A 共线且 ∠COD=20° ， ∠BOC=80° ，射线 OM ， ON 分别平分 ∠AOB 和 ∠BOD ．

    如图2，将射线 OD 以每秒 6° 的速度绕点 O 顺时针旋转一周，同时将 ∠BOC 以每秒 4° 的速度绕点 O 顺时针旋转，当射线 OC 与射线 OA 重合时， ∠BOC 停止运动．设射线 OD 的运动时间为 t ．

           

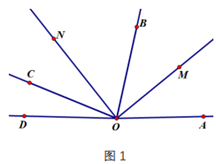
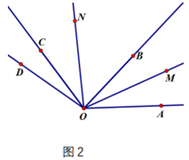    (1)、运动开始前，如图1， ∠AOM= ° ， ∠DON= °
    (2)、旋转过程中，当 t 为何值时，射线 OB 平分 ∠AON ？
    (3)、旋转过程中，是否存在某一时刻使得 ∠MON=35° ？若存在，请求出 t 的值；若不存在，请说明理由．

    查看试题解析