人教版七年级上第二章综合测试卷

试卷更新日期：2022-10-08 类型：单元试卷

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、﹣a+b+c+d=﹣（a﹣b）﹣（﹣c﹣d） B、x﹣（y﹣z）=x﹣y﹣z C、x+2y﹣2z=x﹣2（z+y） D、﹣（x﹣y+z）=﹣x﹣y﹣z

查看试题解析
2. 一个多项式与2x²+2x-1的和是x+2，则这个多项式为（）

A、x²-5x+3 B、-x²+x-1 C、-2x²-x+3 D、x²-5x-13

查看试题解析
3. 如果多项式x^m-3＋5x－3是关于x的三次三项式，那么m的值为（）

A、0 B、3 C、6 D、9

查看试题解析
4. 下列运算中，正确的是（）

A、 $- 1 - 1 = 0$ B、 $- 3 (x - 2 y) = - 3 x - 6 y$ C、 $3 \div 6 \times \frac{1}{2} = 3 \div 3 = 1$ D、 $4 y x^{2} - x^{2} y = 3 y x^{2}$

查看试题解析
5. 如果单项式 $- x y^{b + 1}$ 与 $\frac{1}{2} x^{a + 2} y^{3}$ 是同类项，那么关于 $x$ 的方程 $a x + b = 0$ 的解为（）

A、 $x = 1$ B、 $x = - 1$ C、 $x = 2$ D、 $x = - 2$

查看试题解析
6. 把一个两位数交换十位数字和个位数字后得到一个新的两位数，若将这个新的两位数与原两位数相加，则所得的和一定是（）

A、11的倍数 B、奇数 C、偶数 D、9的倍数

查看试题解析
7. 若x＜0，则-│－x│+|-x-x|等于（）

A、0 B、x C、－x D、以上答案都不对

查看试题解析
8. 已知代数式x²＋ax－2y＋7－(bx²－2x＋9y－1)的值与x的取值无关，则a＋b的值为（）

A、－1 B、1 C、－2 D、2

查看试题解析
9. 某公司有如图所示的甲、乙、丙、丁四个生产基地．现决定在其中一个基地修建总仓库，以方便公司对各基地生产的产品进行集中存储．已知甲、乙、丙、丁各基地的产量之比等于4：5：4：2，各基地之间的距离之比a：b：c：d：e＝2：3：4：3：3（因条件限制，只有图示中的五条运输渠道），当产品的运输数量和运输路程均相等时，所需的运费相等．若要使总运费最低，则修建总仓库的最佳位置为（）

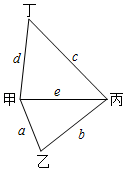A、甲 B、乙 C、丙 D、丁

查看试题解析
10. 把五张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个大长方形(长为m，宽为n内(如图②)，大长方形未被卡片覆盖的部分用阴影表示.当m不变，n变长时，阴影部分的面积差总保持不变，则a，b应满足的关系为（ )

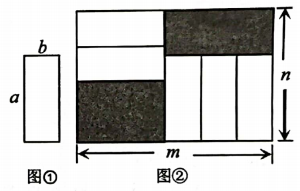A、a=5b B、a=3b C、a=2b D、 $a = \frac{3}{2} b$

查看试题解析

二、填空题

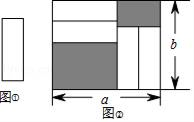
11. 张老师用长 $8 a$ 的铁丝做了一个长方形教具，其中一边长为 $b - a$ ，则另一边的长为.

查看试题解析
12. 若7a^xb²与－3a³b^y的和为单项式，则x^y＝．

查看试题解析
13. 计算： $x^{2} \cdot x^{4} + {(- x^{2})}^{3} =$ .

查看试题解析
14. 单项式 9 $x^{m}$ $y^{3}$ 与单项式 4 $x^{2}$ $y^{n}$ 是同类项，则 ${(m - n)}^{2021}$ ＝.

查看试题解析
15. 在a²+（2k﹣6）ab+b²+9中，不含ab项，则k= ．

查看试题解析
16. 把四张形状大小完全相同的小长方形卡片（如图①），卡片长为x，宽为y，不重叠地放在一个底面为长方形（宽为a）的盒子底部（如图②），盒底面未被卡片覆盖的部分用阴影表示．则图②中两块阴影部分周长和是（用只含b的代数式表示）．

查看试题解析
17. 定义新运算：对于任意实数a、b，都有 $a \otimes b = 13 a - b$ ，则 $x \otimes 1 - x \otimes 2$ 的值为.

查看试题解析
18. 多项式 $4 x^{2} - \frac{π x y^{2}}{2} - \frac{1}{3} x + 1$ 的三次项系数是.

查看试题解析
19. 若两个单项式 $2 a^{2} b^{m - 1}$ 与 $n a^{2} b$ 的和为0，则 $m + n$ 的值是.

查看试题解析
20. 已知某三角形第一条边长为 $（ 3 a - 2 b ）$ cm，第二条边比第一条边长 $（ a + 2 b ）$ cm，第三条边比第一条边的2倍少bcm，则这个三角形的周长为cm．

查看试题解析

三、计算题

21. 化简

(1)、3y²-2y+4y²-7y；

(2)、（2a²- $\frac{1}{2}$ +3a）-（a-a²+ $\frac{1}{2}$ ）；

(3)、 $\frac{1}{3}$ m²n-nm²- $\frac{1}{2}$ mn²+ $\frac{1}{6}$ n²m.

查看试题解析
22. 先化简，再求值： $\frac{1}{2} x - 2 (x - \frac{1}{3} y^{2}) + (- \frac{3}{2} x + \frac{1}{3} y^{2})$ ，其中 $x$ 、 $y$ 满足 $(x - 2)^{2} + | y - 3 | = 0$ ．

查看试题解析

四、解答题

23. 若单项式 $- \frac{1}{3}$ $π$ ⁿy^2n-1的次数是3，求当y=3时此单项式的值．

查看试题解析
24. 先化简下式，再求值：5（3a²b﹣ab²）﹣4（﹣ab²+3a²b），其中a=﹣2，b=3．

查看试题解析
25. 课堂上李老师把要化简求值的整式（7a²﹣6a²b+3a²b）﹣（﹣3a²﹣6a²b+3a²b+10a²﹣3）写完后，让王红同学任意给出一组a、b的值，老师自己说答案，当王红说完：“a=38，b=﹣32”后，李老师不假思索，立刻就说出答案“3”．同学们莫名其妙，觉得不可思议，但李老师用坚定的口吻说：“这个答案准确无误”，亲爱的同学你相信吗？请你通过计算说出其中的道理．

查看试题解析
26. 已知：关于x、 $y$ 的多项式 $x^{2} + a x - y + b$ 与多项式 $b x^{2} - 3 x + 6 y - 3$ 的差的值与字母x的取值无关，求代数式 $3 (a^{2} - 2 a b - b^{2}) - (4 a^{2} + a b + b^{2})$ 的值.

查看试题解析
27. 已知，有理数a，b，c在数轴上的对应点的位置如下图所示，化简： $| c + b | - | a - c | + | b - a |$ ．

查看试题解析

五、综合题

28. 已知A=3a²b-2ab²+abc，2A+B=4a²b-3ab²+4abc.

(1)、计算 $B$ 的表达式；

(2)、求 $2 A - B$ 的表达式；

(3)、小强同学说：“当 $c = 2021$ 时和 $c = - 2021$ 时.（2）中的结果都是一样的”、你认为你对吗？若 $a = \frac{1}{8}$ ， $b = \frac{1}{5}$ .求（2）中式子的值.

查看试题解析