2022-2023年七年级第一学期第一次月考模拟卷（考试范围：第一、二章）（1）

试卷更新日期：2022-10-08 类型：月考试卷

进入出卷网下载

一、单选题

1. 在﹣ $\frac{1}{2}$ ，﹣ $\frac{1}{3}$ ，﹣2，﹣3中，最大的数是（）

A、﹣ $\frac{1}{3}$ B、﹣ $\frac{1}{2}$ C、﹣2 D、﹣1

查看试题解析
2. 在代数式 $x^{2} + 5$ ， $- 1$ ， $3 x = 2$ ， $\frac{x^{2} + 1}{x}$ ， $\frac{x + 1}{3}$ ， $\frac{2 x^{2} - x}{π}$ 中，整式有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
3. 若a、b为有理数，a＜0，b＞0，且|a|＞|b|，那么a，b，﹣a，﹣b的大小关系是（）

A、﹣b＜a＜b＜﹣a B、﹣b＜b＜a＜﹣a C、a＜﹣a＜﹣b＜b D、a＜﹣b＜b＜﹣a

查看试题解析
4. 关于多项式2⁶﹣3x⁵+x⁴+x³+x²+x的说法正确的是（　　）

A、是六次六项式 B、是五次六项式 C、是六次五项式 D、是五次五项式

查看试题解析
5. 下列说法中：（1）整数与分数统称为有理数；（2）如果两个数的绝对值相等，那么这两个数相等；（3）多项式 $2 x^{2} y - x y$ 是五次二项式；（4）倒数等于它本身的数是 $± 1$ ；（5） $3 m^{2} n$ 与 $- n m^{2}$ 是同类项，其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 在数轴上，点M、N分别表示数m，n.则点M、N之间的距离为 $| m - n |$ .已知点A，B，C，D在数轴上分别表示的数为a，b，c，d.且 $| a - c | = | b - c | = 2 ， \frac{2}{5} | d - a | = 1 (a \neq b)$ ，则线段 $B D$ 的长度为（）

A、4.5 B、1.5 C、6.5或1.5 D、4.5或1.5

查看试题解析
7. 六位数由三位数重复构成，如256256，或678678等等，这类数不能被何数整除（）

A、11 B、101 C、13 D、1001

查看试题解析
8. 如果 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ ＝﹣1，那么 $\frac{| a b |}{a b} + \frac{| b c |}{b c} + \frac{| a c |}{a c} + \frac{| a b c |}{a b c}$ 的值为（）

A、﹣2 B、﹣1 C、0 D、不确定

查看试题解析
9. 如图，将图1中的长方形纸片前成（1）号、（2）号、（3）号、（4）号正方形和（5）号长方形，并将它们按图2的方式无重叠地放入另一个大长方形中，若需求出没有覆盖的阴影部分的周长，则下列说法中错误的是（）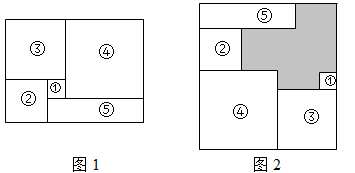

A、只需知道图 1 中大长方形的周长即可 B、只需知道图 2 中大长方形的周长即可 C、只需知道（3）号正方形的周长即可 D、只需知道（5）号长方形的周长即可

查看试题解析
10. 实数a、b在数轴上的位置如图所示，则化简|a+2b|-|a-b|的结果为（）

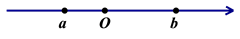A、3b B、2a +b C、-2a-b D、b

查看试题解析

二、填空题

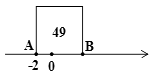
11. 在数轴上点A、点B两点的距离是3，若点A表示-1，则点B表示的数是．

查看试题解析
12. 一个长方形的长为 $8 \times 1 0^{3} c m$ ．宽为 $5 \times 1 0^{2} c m$ 则它的面积为 $c m^{2}$ ．

查看试题解析
13. 下列说法：① $1 - x y$ 是多项式；② $- \frac{2 a b}{3}$ 的系数是 $\frac{2}{3}$ ；③多项式 $x^{2} - x y^{2}$ 的常数项是-1；其中正确的序号是.

查看试题解析
14. 点A，B在数轴上，以AB为边作正方形，该正方形的面积是49．若点A对应的数是－2，则点B对应的数是．

查看试题解析
15. 若|x－y|＋ $\sqrt{y - 2}$ ＝0，则xy＋1的值为.

查看试题解析
16. 已知|a|＝2，b²＝9且a＞b，那么a+b的值是．

查看试题解析
17. 同学们都知道： $| 5 - (- 2) |$ 表示5与-2之差的绝对值，实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离，同理， $| x + 2 | + | x + 3 |$ 可以表示数轴上有理数 $x$ 所对应的点到-2和-3所对应的点的距离之和，则 $| x + 2 | + | x + 3 |$ 的最小值为.

查看试题解析
18. 三个有理数 $a$ ， $b$ ， $c$ ， $a b c < 0$ ， $a + b + c > 0$ ．当 $x = \frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 时， $x^{19} - 92 x + 10$ 的值为．

查看试题解析
19. 计算：1－2－3＋4＋5－6－7＋8＋…＋97－98－99＋100=

查看试题解析
20. 如图所示，在数轴上，点 $A$ 表示1，现将点 $A$ 沿轴做如下移动，第一次点 $A$ 向左移动3个单位长度到达点 $A_{1}$ ，第二次将点 $A_{1}$ 向右移动6个单位长度到达点 $A_{2}$ ，第三次将点 $A_{2}$ 向左移动9个单位长度到达点 $A_{3}$ ，按照这种移动规律移动下去，第 $n$ 次移动到点 $A_{n}$ ，如果点 $A_{n}$ 与原点的距离不小于20，那么 $n$ 的最小值是．

查看试题解析

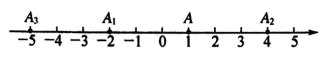
三、计算题

21. 计算：

(1)、 $- 3^{2} - (- 8) \times {(- 1)}^{5} \div {(- 1)}^{4}$ ；

(2)、 $- 1^{2} + {(- 1 \frac{1}{2})}^{3} \div \frac{3}{4} - | 0.25 - \frac{3}{8} |$

(3)、 $(\frac{2}{3} - \frac{3}{4} + \frac{1}{6}) \div (- \frac{1}{24})$

查看试题解析
22. 先化简，再求值：

(1)、3m²-（5m-3＋3m²），其中m＝4.

(2)、﹣2x²﹣[3y²﹣（x²﹣y²）+6]，其中|x+1|+（y﹣1）²＝0.

查看试题解析

四、解答题

23. 有理数a，b，c在数轴上的位置如图所示，试化简|a-b|-|b-c|+2|-a+c|-3|a+b|.

查看试题解析
24. 数轴上到原点的距离小于3的整数的个数为x，不大于3的正整数的个数为y，绝对值等于3的整数的个数为z，求：x+y+z的值．

查看试题解析
25. 若a， $b$ 互为相反数， $c$ ， $d$ 互为倒数，且 $x$ 的绝对值是5，求（a+b+cd）+ $| 3 - x |$ 的值.

查看试题解析
26. 请你先认真阅读材料：
计算 $(- \frac{1}{30}) \div (\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5})$

解：原式的倒数是 $(\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5}) \div (- \frac{1}{30})$

＝ $(\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5}) \times (- 30)$

＝ $\frac{2}{3}$ ×（﹣30）﹣ $\frac{1}{10}$ ×（﹣30）+ $\frac{1}{6}$ ×（﹣30）﹣ $\frac{2}{5}$ ×（﹣30）

＝﹣20﹣（﹣3）+（﹣5）﹣（﹣12）

＝﹣20+3﹣5+12

＝﹣10

故原式等于﹣ $\frac{1}{10}$

再根据你对所提供材料的理解，选择合适的方法计算： $(- \frac{1}{42}) \div (\frac{1}{6} - \frac{3}{14} + \frac{2}{3} - \frac{2}{7})$ ．

查看试题解析
27. 某出租车沿南北方向行驶，从A地出发，晚上到达B地．规定向北为正方向．行驶记录如下（单位：㎞）：+18、-9、+7、-14、-6、+13、-6，

(1)、B地在A地的什么位置？

(2)、若出租车每行驶1㎞耗油1升，求该天共耗油多少升？

(3)、若出租车起步价为7元，起步里程为3千米（包括3千米），超过部分每千米1.2元，则该天车费多少元？

查看试题解析