2022-2023学年四川省九年级上学期第一次月考数学模拟试卷

试卷更新日期：2022-10-07 类型：月考试卷

进入出卷网下载

一、单选题（每题4分，共40分）

1. 下列方程中，是一元二次方程的是（）

A、ax²+bx+c＝0 B、x²+ $\frac{1}{x}$ ＝1 C、x²﹣1＝0 D、2x+3y﹣5＝0

查看试题解析
2. 下列一元二次方程中，有一个根为1的方程是（）

A、 $x^{2} - 2 x + 3 =0$ B、 $x^{2} - 3 x + 2=0$ C、 $x^{2} - 2 x - 3 =0$ D、 $x^{2} + 3 x - 2 =0$

查看试题解析
3. 将一元二次方程3x²﹣2x＝6化为一般形式，若二次项系数为3，则一次项系数和常数项分别为（）

A、﹣2，6 B、﹣2，﹣6 C、2，6 D、2，﹣6

查看试题解析
4. 一元二次方程 $x^{2} - 4 = 0$ 的根为（）

A、 $x = - 2$ B、 $x = 2$ C、 $x = \pm 2$ D、 $x = \pm \sqrt{2}$

查看试题解析
5. 若关于x的一元二次方程 $(a - 6) x^{2} - 2 x + 3 = 0$ 有实数根，则整数a的最大值是（）

A、4 B、5 C、6 D、7

查看试题解析
6. 等腰三角形一边长为2，它的另外两条边的长度是关于x的一元二次方程x²﹣6x+k＝0的两个实数根，则k的值是（）

A、8 B、9 C、8或9 D、12

查看试题解析
7. 一元二次方程x²﹣3x+1＝0的两个根为x₁ ， x₂ ，则x₁²+3x₂+x₁x₂﹣2的值是（）

A、10 B、9 C、8 D、7

查看试题解析
8. 肆虐的冠状病毒肺炎具有人传人性，调查发现：1人感染病毒后如果不隔离，那么经过两轮传染将会有225人感染，若设1人平均感染x人，依题意可列方程（）

A、1+x＝225 B、1+x²＝225 C、（1+x）²＝225 D、1+（1+x² ）＝225

查看试题解析
9. 某商场将进价为 $20$ 元∕件的玩具以 $30$ 元∕件的价格出售时，每天可售出 $300$ 件，经调查当单价每涨 $1$ 元时，每天少售出 $10$ 件．若商场想每天获得 $3750$ 元利润，则每件玩具应涨多少元？若设每件玩具涨 $x$ 元，则下列说法错误的是（）

A、涨价后每件玩具的售价是 $(30 + x)$ 元 B、涨价后每天少售出玩具的数量是 $10 x$ 件 C、涨价后每天销售玩具的数量是 $(300 - 10 x)$ 件 D、可列方程为 $(30 + x) (300 - 10 x) = 3750$

查看试题解析
10. 对于一元二次方程ax²+bx+c＝0（a≠0），下列说法：①若a+b+c＝0，则b²﹣4ac≥0；②若方程ax²+c＝0有两个不相等的实根，则方程ax²+bx+c＝0必有两个不相等的实根；③若c是方程ax²+bx+c＝0的一个根，则一定有ac+b+1＝0成立；④若x₀是一元二次方程ax²+bx+c＝0的根，则 $b^{2} - 4 a c = {(2 a x_{0} + b)}^{2}$ ；其中正确的（）

A、只有①② B、只有①②④ C、①②③④ D、只有①②③

查看试题解析

二、填空题（每题4分，共24分）

11. 一元二次方程 $x^{2} - 3 x = 0$ 的根是．

查看试题解析
12. 若一元二次方程2x²﹣3x+1＝0的两个实数根为x₁ ， x₂ ，则x₁²+x₂²﹣x₁•x₂的值是．

查看试题解析
13. 若关于x的一元二次方程 $x^{2} + x - m = 0$ 有两个实数根，则m的取值范围是．

查看试题解析
14. 已知m是方程x²-x-1=0的一个根，则代数式5m²-5m+2015的值为

查看试题解析
15. 已知一个三角形的三边都是方程 $x^{2} - 8 x + 12 = 0$ 的根，则此三角形的周长为．

查看试题解析
16. 若 $x^{2} + 3 x = - 1$ ，则 $x - \frac{1}{x + 1} =$ ．

查看试题解析

三、解答题（共9题，共86分）

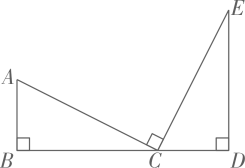
17. 请选择适当的方法解下列一元二次方程：

(1)、 $2 x^{2} + 6 x + 3 = 0$ ；

(2)、 ${(x + 2)}^{2} = 3 (x + 2)$ .

查看试题解析
18. 先化简，再求值： $(\frac{1}{x + 1} - 1) \div \frac{x^{2} - x}{x + 1}$ ，其中 $x = \sqrt{2} + 1$ ．

查看试题解析
19. 如图，点C在线段BD上，且AB⊥BD，DE⊥BD，AC⊥CE，BC=DE，求证：AB=CD．

查看试题解析
20. 已知 $x_{1}$ ， $x_{2}$ 是一元二次方程 $x^{2} - 2 x + k + 2 = 0$ 的两个实数根．

(1)、求k的取值范围；

(2)、是否存在实数k，使得等式 $\frac{1}{x_{1}} + \frac{1}{x_{2}} = k - 2$ 成立？如果存在，请求出k的值，如果不存在，请说明理由．

查看试题解析
21. 今年某商店“十一黄金周”进行促销活动期间，前六天的总营业额为450万元，第七天的营业额是前六天总营业额的12%、今年该商店7月份的营业额为350万元，8、9月份营业额的月增长率相同，“十一黄金周”这七天的总营业额与9月份的营业额相等，求该商店今年8、9月份营业额的月增长率．

查看试题解析
22. 已知关于 $x$ 的方程 $x^{2} + (m + 2) x + 2 m - 1 = 0$ .

(1)、求证：方程有两个不相等的实数根.

(2)、当 $m$ 为何值时，方程的两根互为相反数？并求出此时方程的解.

查看试题解析
23. 在宽为20m，长为32m的矩形地面上修筑同样宽的道路（图中阴影部分），余下的部分种上草坪．要使草坪的面积为540m² ，求道路的宽．

查看试题解析
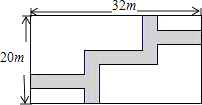24. 一学校为了绿化校园环境，向某园林公司购买了一批树苗，园林公司规定：如果购买树苗不超过60棵，每棵售价120元；如果购买树苗超过60棵，每增加1棵，所出售的这批树苗每棵售价均降低0.5元，但每棵树苗最低售价不得少于100元，该校最终向园林公司支付树苗款8800元，请问该校共购买了多少棵树苗？

查看试题解析
25. 如果关于 $x$ 的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 有两个实数根，且其中一个根为另一个根的 $2$ 倍，那么称这样的方程为“倍根方程”，例如，一元二次方程 $x^{2} - 6 x + 8 = 0$ 的两个根是 $2$ 和 $4$ ，则方程 $x^{2} - 6 x + 8 = 0$ 就是“倍根方程”．

(1)、若一元二次方程 $x^{2} - 3 x + c = 0$ 是“倍根方程”，则c＝．

(2)、若关于x的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 是“倍根方程”，则 $a$ ， $b$ ， $c$ 之间的关系为．

(3)、若 $(x - 2) (m x - n) = 0 (m \neq 0)$ 是“倍根方程”，求代数式 $4 m^{2} - 5 m n + n^{2}$ 的值．

查看试题解析