2022-2023学年浙教版数学七上期中复习专题3 绝对值

试卷更新日期：2022-10-07 类型：复习试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. ﹣ |-2| 的值是（）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、- $\frac{1}{2}$

查看试题解析

2. 小红和她的同学共买了6袋标准质量为

450 g

的食品，她们对这6袋食品的实际质量进行了检测，检测结果（用正数记超过标注质量的克数，用负数记不足标准质量的克数）如下：

第一袋	第二袋	第三袋	第四袋	第五袋	第六袋
-25	+10	-20	+30	+15	-40

食品质量最接近标准质量的是第几袋?最重的是第几袋? （）

A、二，四 B、六，四 C、一，六 D、二，六

查看试题解析

3. 如图，数轴上的点A所表示的数为a，化简|a|﹣|a﹣4|的结果为（）

A、﹣2a﹣4 B、﹣4 C、2a+4 D、4

查看试题解析
4. 实数a，b，c在数轴上的对应点的位置如图所示，若|a|>|b|，则下列结论中一定成立的是（）

A、b+c>0 B、a+c<-2 C、 $\frac{b}{a}$ <1 D、abc≥0

查看试题解析
5. 下列说法中错误的是（　　）

A、如果a＞0，b＜0且a+b＞0，则|a|＞|b| B、如果a＜0，b＞0，则a-b＜0 C、如果a+b＜0，且a，b同号，那么a＞0，b＞0 D、如果a＜0，b＜0且|a|＞|b|，则a-b＜0

查看试题解析
6. 如果x是有理数，那么下列各式中一定比0大的是（）

A、2021x B、2021+x C、|x|+2021 D、|x|

查看试题解析
7. 对于任何有理数a，下列一定为负数的是（）

A、 $- \sqrt{a^{2}}$ B、 $- | a | - 1$ C、 $- | a + 1 |$ D、 $- {(a - \frac{1}{2})}^{2}$

查看试题解析
8. 数轴上的A，B，C三点所表示的数分别为a、b、1，且|a﹣1|+|b﹣1|＝|a﹣b|，则下列选项中，满足A，B，C三点位置关系的数轴为（）

A、 B、 C、 D、

查看试题解析
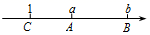9. 小明做这样一道题“计算：|（﹣3）+■|”，其中“■”是被墨水污染看不清的一个数，他翻开后面的答案知该题计算的结果是等于6，那么“■”表示的数是（）

A、3 B、﹣3 C、9 D、﹣3或9

查看试题解析
10. 已知 $a, b$ 表示两个非零的实数，则 $\frac{| a |}{a} + \frac{| b |}{b}$ 的值不可能是（）

A、2 B、–2 C、1 D、0

查看试题解析

二、填空题（每空2分，共14分）

11. 计算： $| 1 - 5 |$ = ．

查看试题解析
12. 已知|a|＝3，|b|＝8，a＞b，则b﹣a的值为 .

查看试题解析
13. 若a是有理数，则|a+1|-2的最小值是，此时a²⁰¹⁶=.

查看试题解析
14. 已知 $| x | = 3$ ， $| y | = 2$ ，且 $| x - y | = y - x$ ，则 $x - y =$

查看试题解析
15. 已知a，b，c，d分别是一个四位数的千位，百位，十位，个位上的数字，且低位上的数字不小于高位上的数字，当|a-b|+|b-c|+|c-d|+|d-a|取得最大值时，这个四位数的最小值是.

查看试题解析
16. 已知整数 $a ， b ， c ， d$ 的绝对值均小于5，且满 $1000 a + 100 b^{2} + 10 c^{3} + d^{4} ＝$ 2021，则 $a b c d$ 的值为．

查看试题解析

三、解答题（共6题，共56分）

17. 数a在数轴上的位置如图，且|a+1|=2，求|3a+7|．

查看试题解析
18. 已知A，B，C三点在数轴上的位置如图所示，它们表示的数分别是a，b，c．

(1)、填空：abc0，a+b0（填“＞”“＜”或“＝”）；

(2)、化简： $| a - b | - 2 | a + b | + | b - c |$ ．

查看试题解析
19. 点A、B在数轴上分别表示数a，b，A、B两点之间的距离表示为|AB|．数轴上A、B两点之间的距离|AB|=|a-b|
回答下列问题：

(1)、数轴上表示－1和－4的两点之间的距离是；

(2)、数轴上表示x和－1的两点A之和B之间的距离是，如果|AB|＝2，那么x的值是；

(3)、若x表示一个有理数，且﹣1＜x＜3，则|x﹣3|+|x+1|=；

(4)、若x表示一个有理数，且|x﹣1|+|x+2|＞3，则有理数x的取值范围是.

查看试题解析
20.

(1)、数轴上表示4与-2的点之间的距离为；数轴上表示3与5的点之间的距离为.

(2)、； .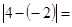

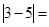(3)、观察（1）（2）两小题，若数轴上的点A表示的数为x ，点B表示的数为y，则A与B两点间的距离可以表示为． A与表示-2的点之间的距离可表示为 .

(4)、结合数轴，求 $| x - 2 | + | x + 3 |$ 的最小值为.

查看试题解析
21. 同学们都知道 $| 5 - (- 2) |$ 表示5与﹣2的差的绝对值，实际上 $| 5 - (- 2) |$ 也理解为5与﹣2这两个数在数轴上对应的两个点之间的距离.即：如果点A在数轴上对应的数是a，点B在数轴上对应的数是b，那么A、B这两个点在数轴上的距离就为 $| a - b |$ .
请认真阅读以上信息，然后回答下列问题：

(1)、 $| x + 2 |$ 表示数轴上的数x与数之间的距离.

(2)、试用数轴探究：若 $| x + 2 | = 4$ ，则x=

(3)、进一步探究：求|x+5|+|x-1|的最小值，并说明理由.

查看试题解析
22. 我们知道：在研究和解决数学问题时，当问题所给对象不能进行统一研究时，我们就需要根据数学对象的本质属性的相同点和不同点，将对象区分为不同种类，然后逐类进行研究和解决，最后综合各类结果得到整个问题的解决，这一思想方法，我们称之为“分类讨论的思想”这一数学思想用处非常广泛，我们经常用这种方法解决问题.例如：我们在讨论|a|的值时，就会对a进行分类讨论，当a≥0时，|a|＝a；当a＜0时，|a|＝﹣a.现在请你利用这一思想解决下列问题：

(1)、 $\frac{8}{| 8 |} =$ ； $\frac{- 3}{| - 3 |} =$ ；

(2)、 $\frac{a}{| a |} =$ （a≠0）， $\frac{a}{| a |} + \frac{b}{| b |} =$ （其中a＞0，b≠0）；

(3)、若abc≠0，试求 $\frac{a}{| a |} + \frac{b}{| b |} + \frac{c}{| c |} + \frac{a b c}{| a b c |}$ 的所有可能的值.

查看试题解析